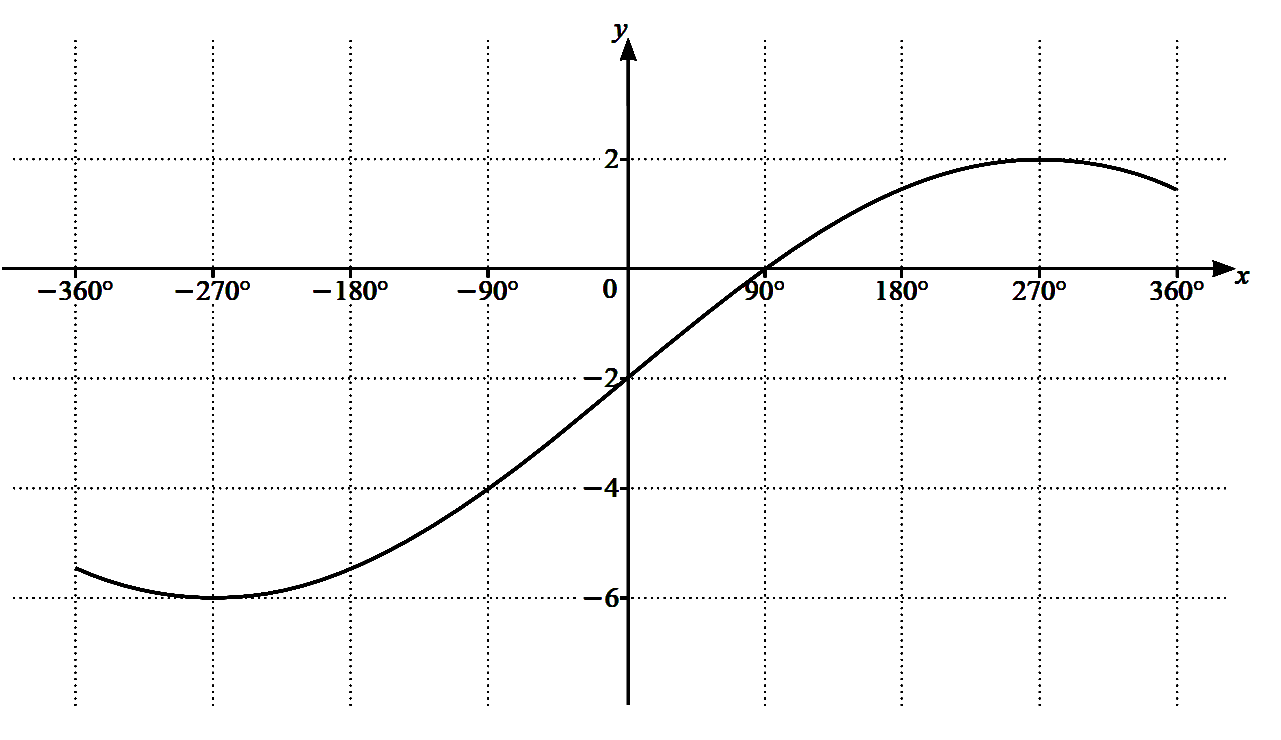-
The diagram shows the graph of $y=a \sin \dfrac{x}{b}+c$ for $-360^{\circ} \le x \le 360^{\circ}$,
(a) Write down the period of $a \sin \dfrac{x}{b}+c$. [1]
(b) Find the value of $a$, of $b$ and of $c$. [3] -
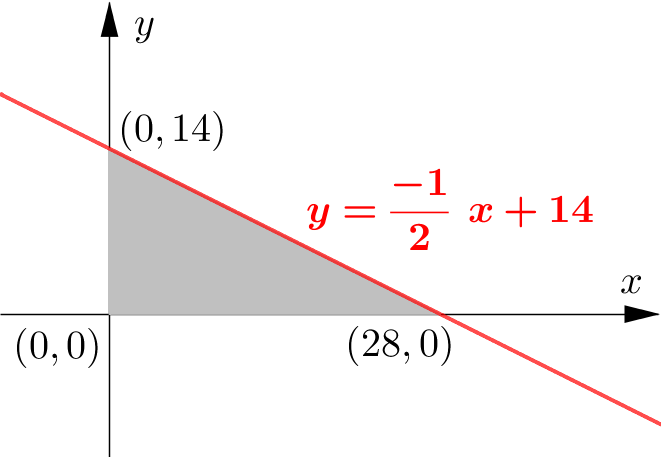
Points $A$ and $C$ have coordinates $(-4, 6)$ and $( 2, 18)$ respectively. The point $B$ lies on the line $A C$ such that $\overrightarrow{A B}=\dfrac{2}{3} \overrightarrow{A C}$.
(a) Find the coordinates of $B$. [2]
(a) Find the equation of the line $l$, which is perpendicular to $AC$ and passes through B. [2]
(c) Find the area enclosed by the line $l$ and the coordinate axes. [2] -
(a) Find the vector which has magnitude $39$ and is in the same direction as $\left(\begin{array}{r}12 \\ -5\end{array}\right)$. [2]
(b) Given that $\mathbf{a}=\left(\begin{array}{r} 2 \\ -1 \end{array}\right)$ and $\mathbf{b}=\left(\begin{array}{r} -4 \\ 5 \end{array}\right)$, find the constants $\lambda$ and $\mu$ such that $5 \mathbf{a}+\lambda\left(\begin{array}{l} 4 \\ 6 \end{array}\right)=\mu \mathbf{b}$ [4] -
(a) Given that $\dfrac{q^{-2} \sqrt{p r}}{\sqrt[3]{r}(p q)^{-3}}=p^{a} q^{b} r^{c}$, find the value of each of the constants $a, b$ and $c$. [3]
(b) Solve the equation $3 x^{\frac{4}{5}}-8 x^{\frac{2}{5}}+5=0$. [4] -
The polynomial $\mathrm{p}(x)=a x^{3}+b x^{2}+6 x+4$, where $a$ and $b$ are integers, is divisible by $x-2$. When $\mathrm{p}^{\prime}(x)$ is divided by $x+1$ the remainder is $-7$.
(a) Find the value of $a$ and of $b$. [5]
(b) Using your answers to part (a), find the remainder when $\mathrm{p}^{\prime \prime}(x)$ is divided by $x$. [2] -
A curve with equation $y=f(x)$ is such that $\dfrac{\mathrm{d}^{2} y}{\mathrm{~d} x^{2}}=6 \mathrm{e}^{3 x}+4 x$. The curve has a gradient of 5 at the point $\left(0, \dfrac{5}{3}\right)$. Find $f(x)$. [7]
-
The first three terms, in ascending powers of $x$, in the expansion of $(2+a x)^{n}$ can be written as $64+b x+c x^{2}$, where $n, a, b$ and $c$ are constants.
(a) Find the value of $n$. [1]
(b) Show that $5 b^{2}=768 c$. [4]
(c) Given that $b = 12$, find the exact value of $a$ and of $c$. [2] -
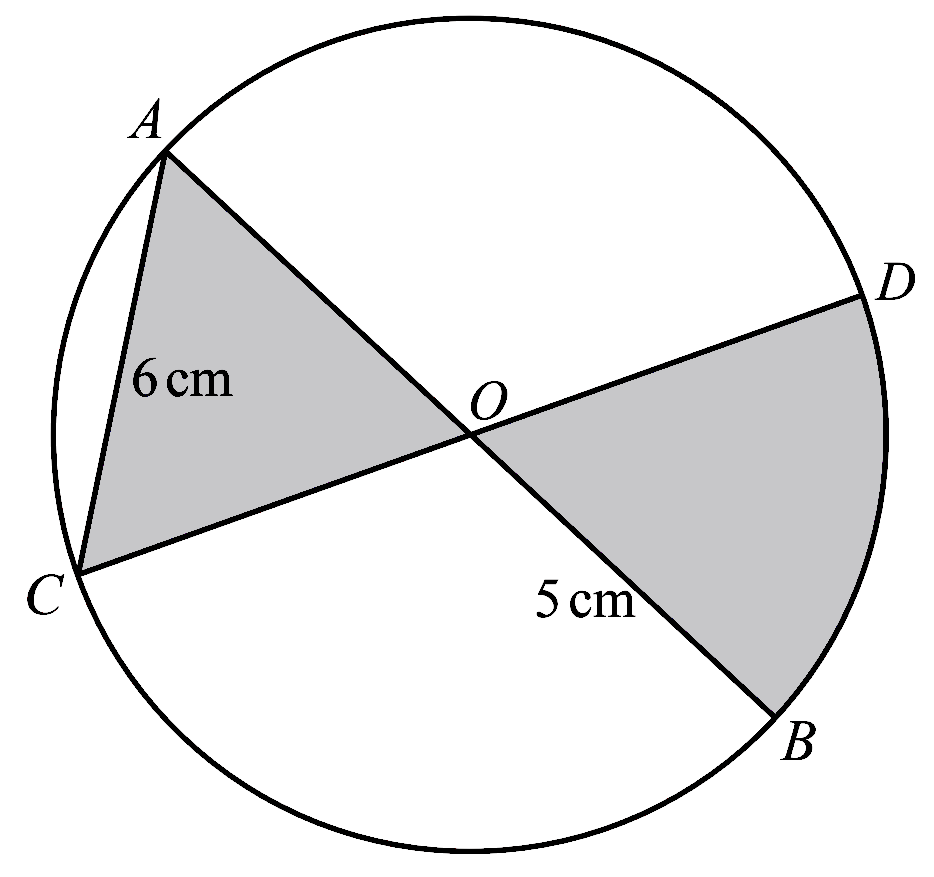
The diagram shows a circle, centre $O$, radius $5$ cm. The lines $AOB$ and $COD$ are diameters of this circle. The line $AC$ has length $6$ cm.
(a) Show that angle $AOC = 1.287$ radians, correct to $3$ decimal places. [2]
(b) Find the perimeter of the shaded region. [2]
(c) Find the area of the shaded region. [3] -
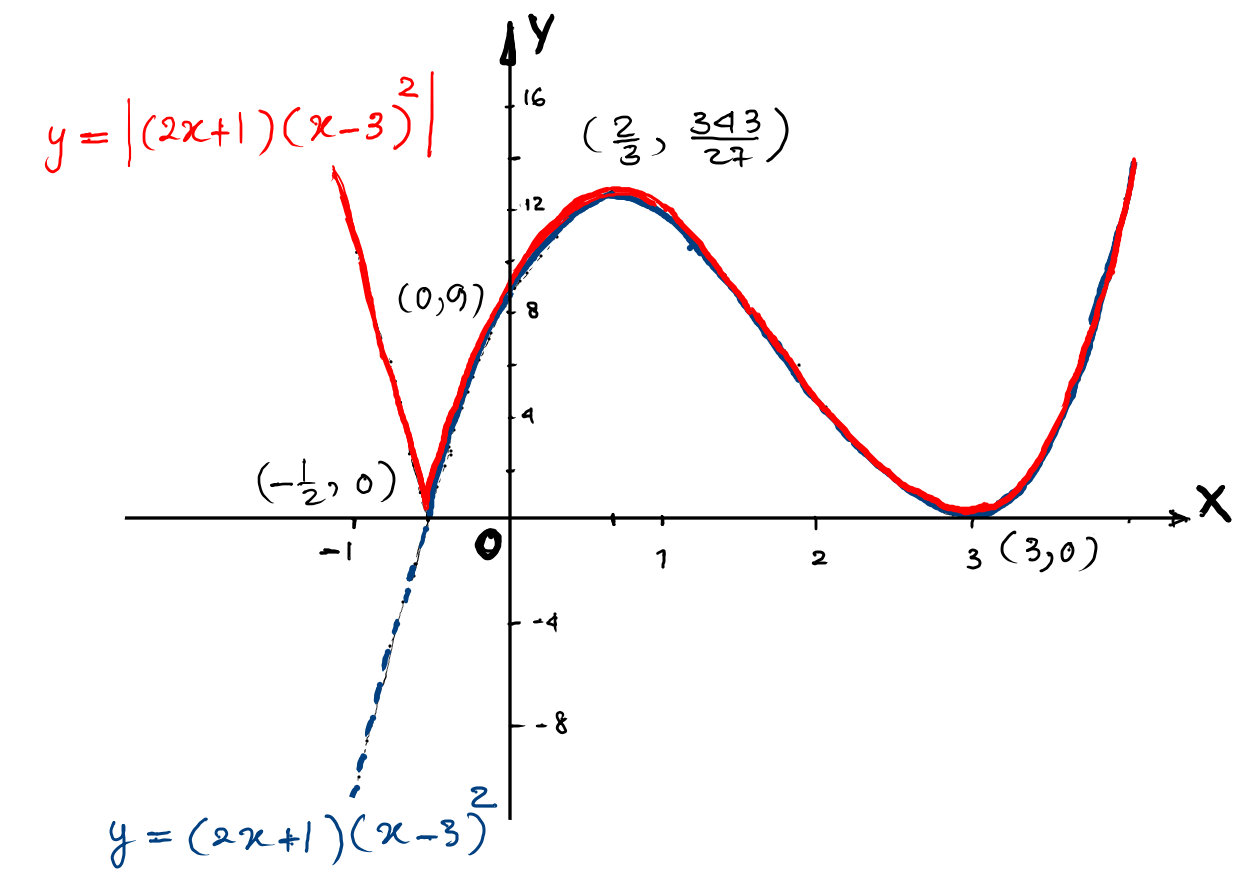
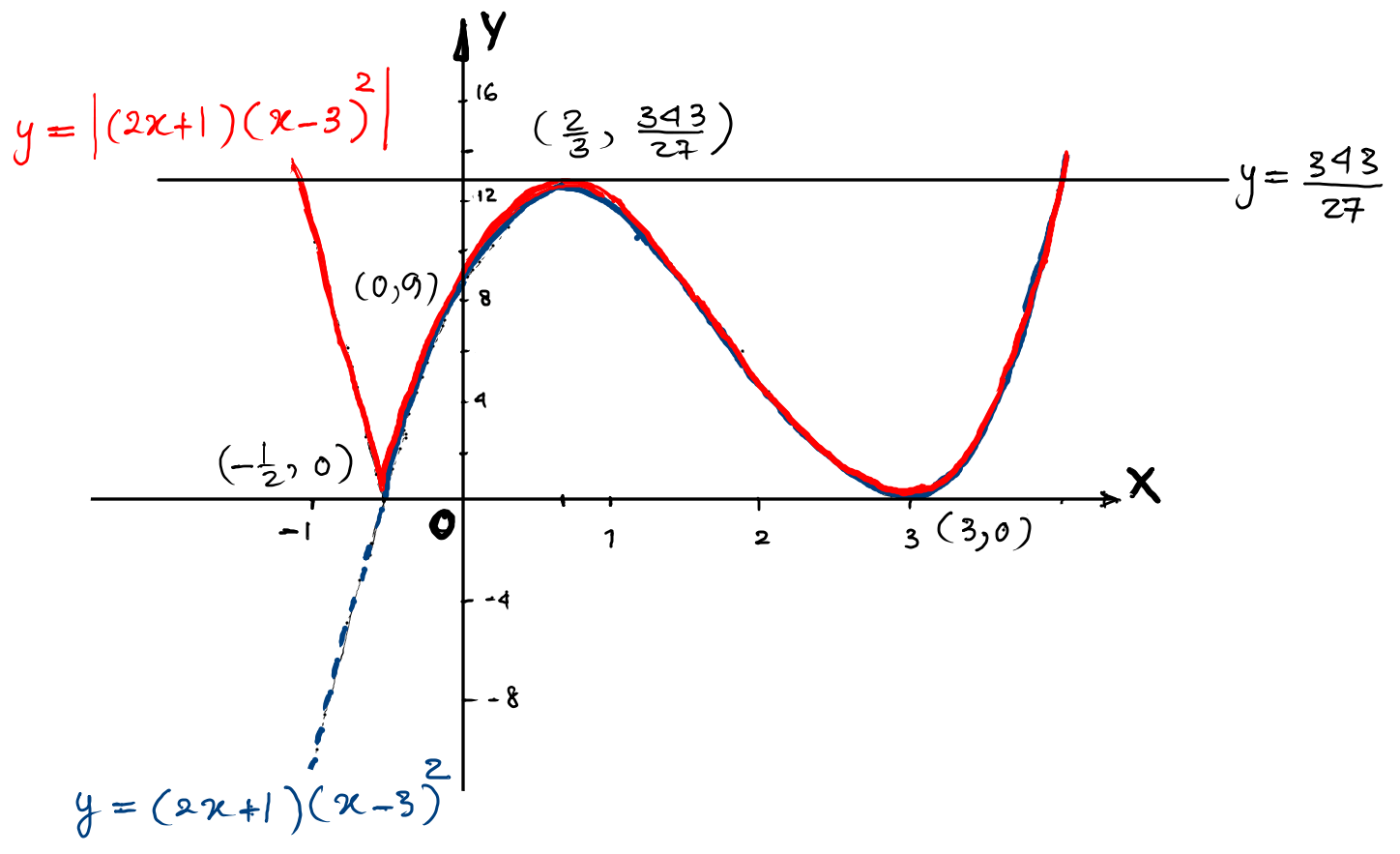
(a) Find the coordinates of the stationary points on the curve $y=(2 x+1)(x-3)^{2}$. Give your answers in exact form. [4]
(b) On the axes below, sketch the graph of $y=\left|(2 x+1)(x-3)^{2}\right|,$ stating the coordinates of the points where the curve meets the axes. [4]
(c) Hence write down the value of the constant $k$ such that $\left|(2 x+1)(x-3)^{2}\right|=k $ has exactly 3 distinct solutions. [1] -
(a) Jess runs on 5 days each week to prepare for a race.
In week 1 , every run is $2$ km.
In week 2, every run is $2.5 $ km.
In week 3 , every run is $3 $ km.
Jess increases the distance of the run by $0.5 $ km every week.
(i) Find the week in which Jess runs $16 $ km on each of the $5$ days. [3]
(ii) Find the total distance Jess will have run by the end of week $8$.
[3] (b) Kyle also runs on 5 days each week to prepare for a race.
In week 1 , every run is $2 $ km.
In week 2, every run is $2.5 $ km.
In week 3, every run is $3.125 $ km.
The distances he runs each week form a geometric progression.
(i) Find the common ratio of the geometric progression. [3]
(ii) Find the first week in which Kyle will run more than $16$ km on each of the $5$ days. [3]
(iii) Find the total distance Kyle will have run by the end of week $8$. [3]
-
(a) Solve the equation $3 \operatorname{cosec}^{2} \theta-5=5 \cot \theta$ for $0^{\circ} \le \theta \le180^{\circ}$. [4]
(b) Solve the equation $\sin \left(\phi+\dfrac{\pi}{3}\right)=-\dfrac{1}{2}$, where $\phi$ is in radians and $-\pi \le \phi \le \pi$. Give your answers in terms of $\pi$. [4]