Roots of a Function
A root of a function is a value of $x$ for which $f(x)=0$. The graph of $y=f(x)$ will cross the $x$-axis at points corresponding to the roots of the function.
$f(x)=0$ ကို ပြေလည်စေသော $x$ တန်ဖိုးများကို $f(x)$ ၏ root ဟုခေါ်သည်။ $f(x)$ ၏ root များသည် $y=f(x)$ ဆိုသော graph က $x$ ဝင်ရိုးကို ဖြတ်သွားသော ဖြတ်မှတ်များ ($x$-intercepts) နှင့် အတူတူပင်ဖြစ်သည်။
Continuous Function
A function is continuous when its graph is a single unbroken curve.
ပေးထားသော domain အတွင်း function တစ်ခု၏ graph သည် ပြတ်တောက်နေခြင်းမရှိလျှင် ၎င်း function ကို continuous ခေါ်သည်။
 |
 |
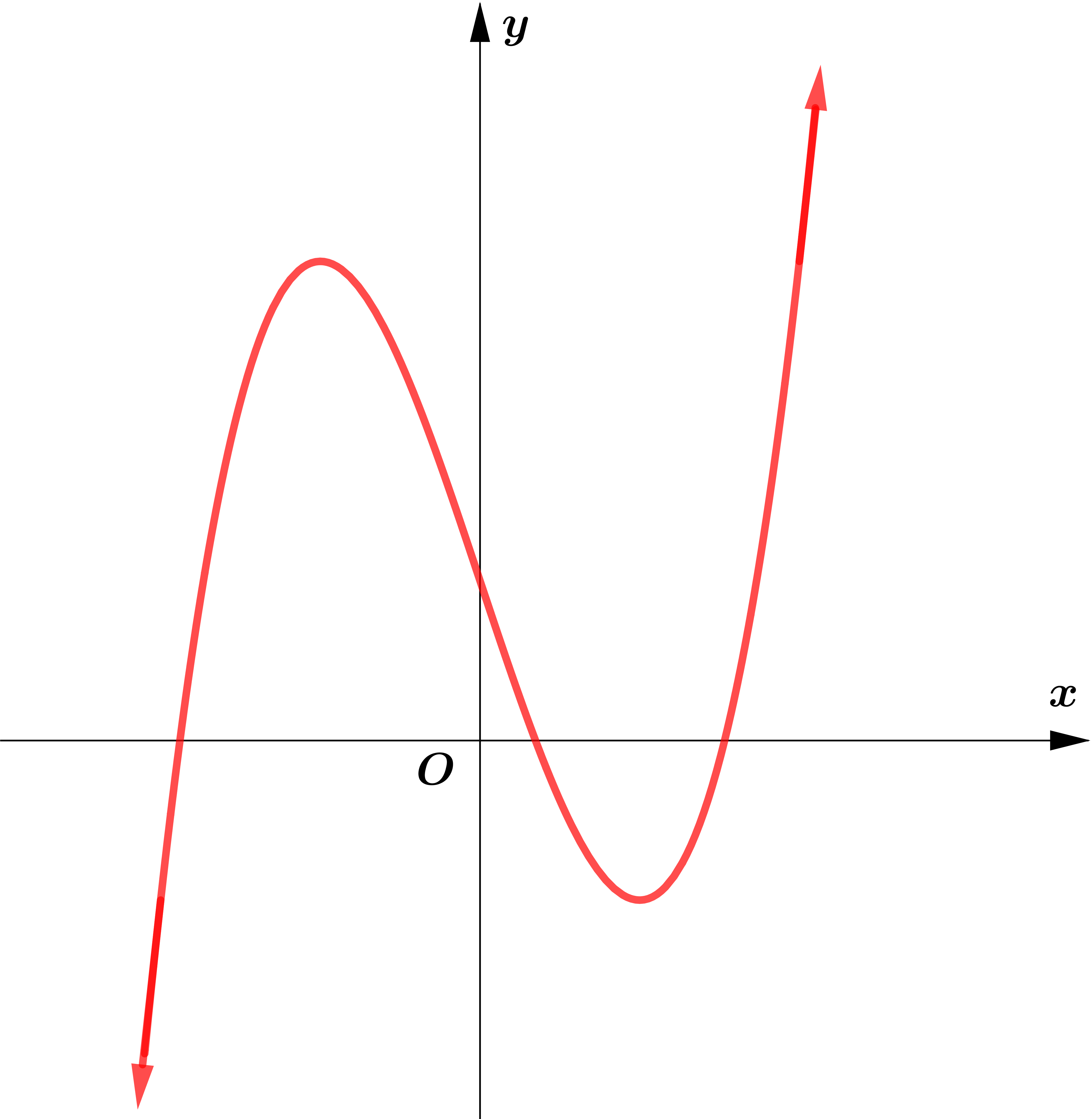
Location of Roots
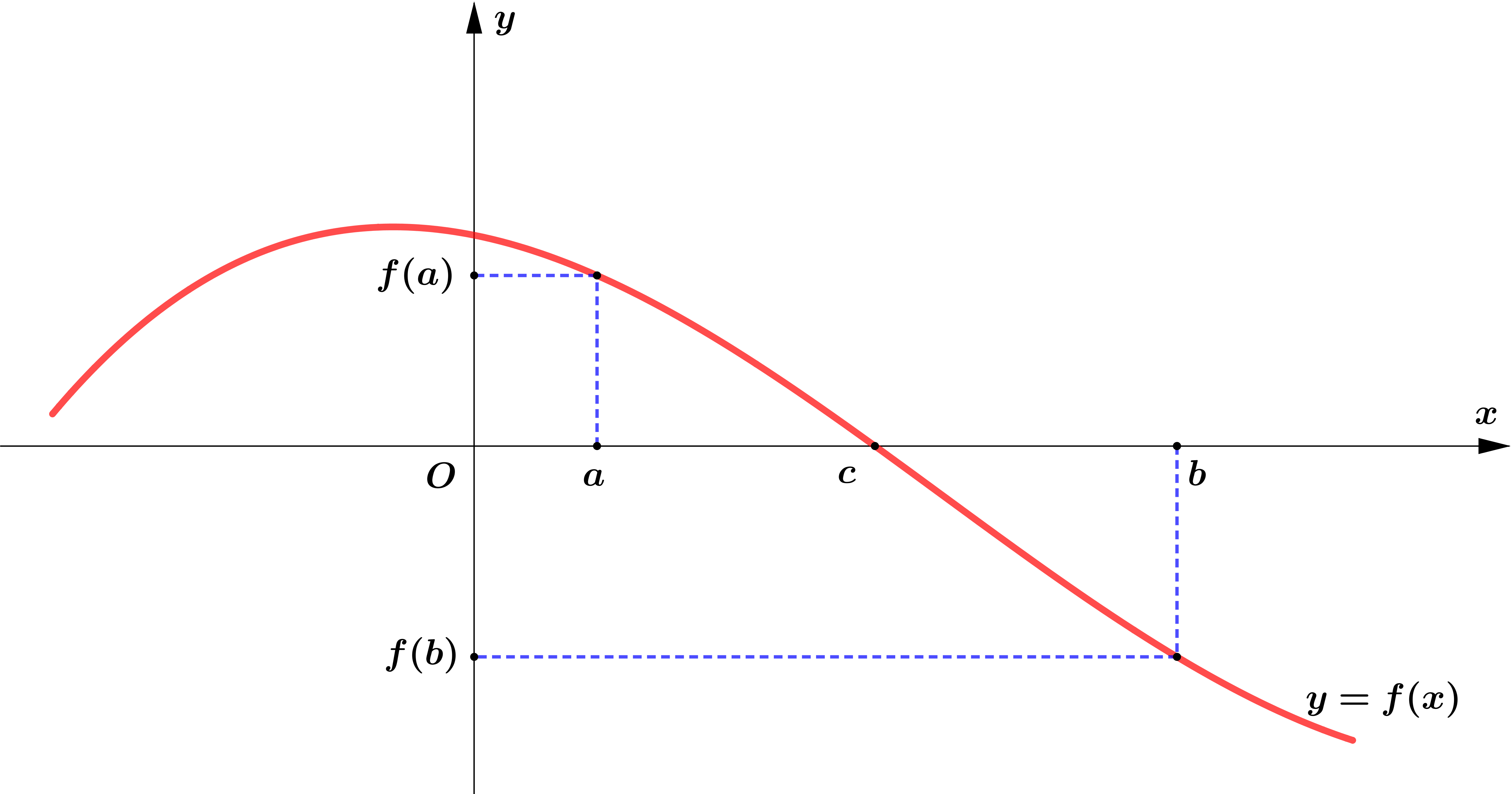
အထက်ဖော်ပြပါပုံတွင် $f(c)=0$ ဖြစ်သည်။ ထို့ကြောင့် $c$ သည် $f(x)=0$ ၏ root ဖြစ်သည်။
graph အရ $f(a) > 0$ ဖြစ်ပြီး $f(b) < 0$ ဖြစ်သည်။
ထို့ကြောင့် အောက်ပါမှန်ကန်ချက်ကို ကောက်ချက်ဆွဲနိုင်သည်။
If the function $f(x)$ is continuous on the interval $[a, b]$ and $f(a)$ and $f(b)$ have opposite signs, then $f(x)$ has at least one root, $x$, which satisfies $a < x < b$.
ကြားပိုင်း $a$ နှင့် $b$ အတွင်း $f(x)$ သည် continuous ဖြစ်ပြီး $f(a)$ ၏ လက္ခဏာနှင့် $f(b)$ ၏ လက္ခဏာ ဆန့်ကျင်ဘက်ဖြစ်လျှင် $f(x)=0$ ဖြစ်စေသော $x$ တန်ဖိုး (root) အနည်းဆုံးတစ်ခု ရှိသည်။
Notice
- $f(a)$ ၏ လက္ခဏာနှင့် $f(b)$ ၏ လက္ခဏာ ဆန့်ကျင်ဘက်ဖြစ်လျှင် root တစ်ခုအနည်းဆုံးရှိသည် ဆိုသည်မှာ တစ်ခုသာရှိသည်ဟု မဆိုလို။ တစ်ခုထက်ပိုမို၍လည်း ရှိနိုင်သည်။
- $f(a)$ ၏ လက္ခဏာနှင့် $f(b)$ ၏ လက္ခဏာ ဆန့်ကျင်ဘက်ဖြစ်လျှင် root တစ်ခုအနည်းဆုံးရှိသည် ဆိုသည်မှာ လက္ခဏာမပြောင်းလျှင် root လုံးဝမရှိဟု မဆိုလိုပါ။တစ်ခုထက်ပိုမို၍လည်း ရှိနိုင်သည်။
- root ၏ တည်နေရာကို ခန့်မှန်းခြင်းသည် root တန်ဖိုးကို ရှာယူခြင်းမဟုတ်ပါ။
- အချို့သော ညီမျှခြင်းများသည် သင်္ချာဆိုင်ရာ လုပ်ထုံးများဖြင့် ဖြေရှင်းရန် အလွန်ခက်ခဲသော အခြေအနေမျိုးရှိတတ်သည်။ ထိုသို့သော အခြေအနေတွင် root ၏ တည်နေရာကို ခန့်မှန်းနိုင်ပြီဆိုပါက root ရရန်နည်းစပ်ပြီဟု ဆိုနိုင်သည်။
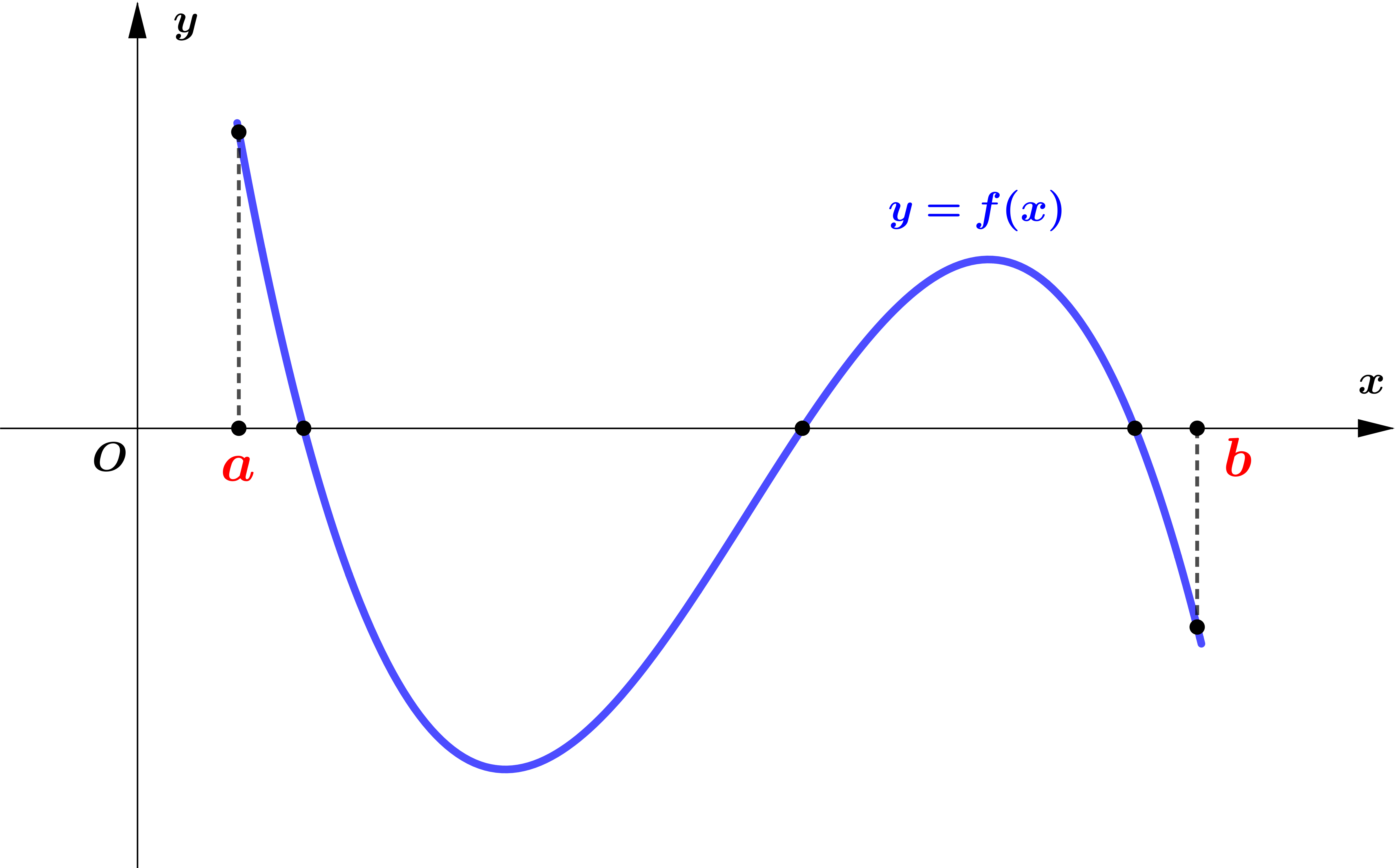 |
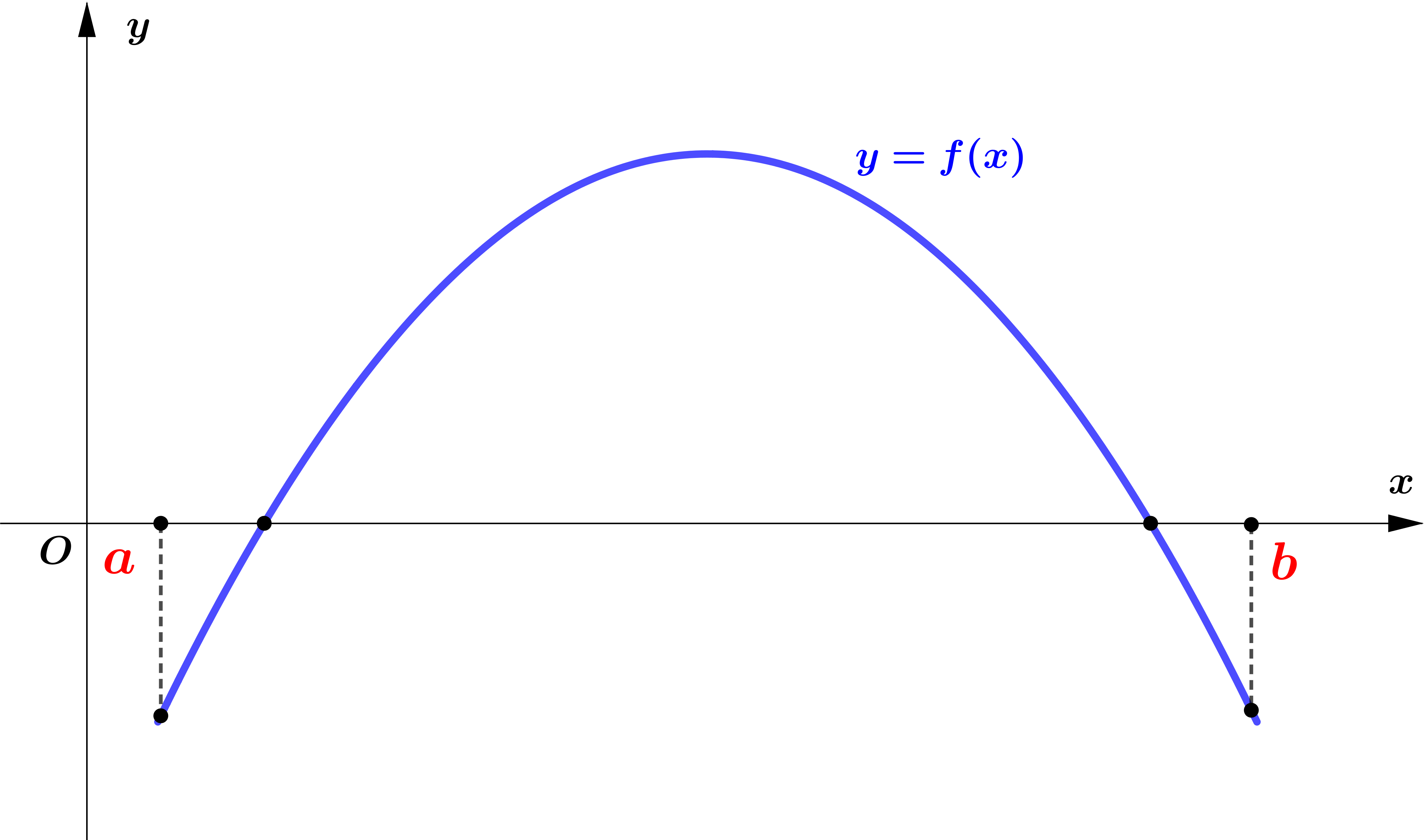 |
| $f(a)>0$ ဖြစ်ပြီး $f(b)< 0$ ဖြစ်သည်။ လက္ခဏာပြောင်းသည်။ ဤသို့သော အခြေအနေတွင် root အရေအတွက်မှာ မ ဂဏန်းဖြစ်သည်။ | $f(a)< 0$ ဖြစ်ပြီး $f(b)< 0$ ဖြစ်သည်။ လက္ခဏာမပြောင်းပါ။ ဤသို့သော အခြေအနေတွင် root အရေအတွက်မှာ စုံ ဂဏန်းဖြစ်သည်။ |
To Find Approximate Solution from Root Loaction (Iterative Method)
$2x^2-x-2=0, x< 0$ ၏ approximate solution ကို ရှာကြည့်ပါမည်။
ပေးထားသော ညီမျှခြင်းကို အောက်ပါအတိုင်း ပြင်ရေးကြည့်မည်။
$\begin{aligned} 2x^2-x-2&=0\\\\ 2x^2-x&=2\\\\ x^2-\frac{1}{2}x&=1\\\\ x\left( x-\frac{1}{2}\right)&=1\\\\ x&=\frac{1}{x-\frac{1}{2}}\\\\ \end{aligned}$ထို့ကြောင့် $2x^2-x-2=0$ ၏ အဖြေသည် $y=x$ နှင့် $y=\dfrac{1}{x-\frac{1}{2}}$ တို့၏ ဖြတ်မှတ်ကို ရှာယူခြင်းနှင့် အတူတူပင်ဖြစ်သည်။
$F(x)=y=\dfrac{1}{x-\frac{1}{2}}$ ဟုသတ်မှတ်သည်ဆိုပါစို့။ ထိုအခါပေးတားသော ညီမျှခြင်းများသည် $x=F(x)$ ဖြစ်လာမည်။
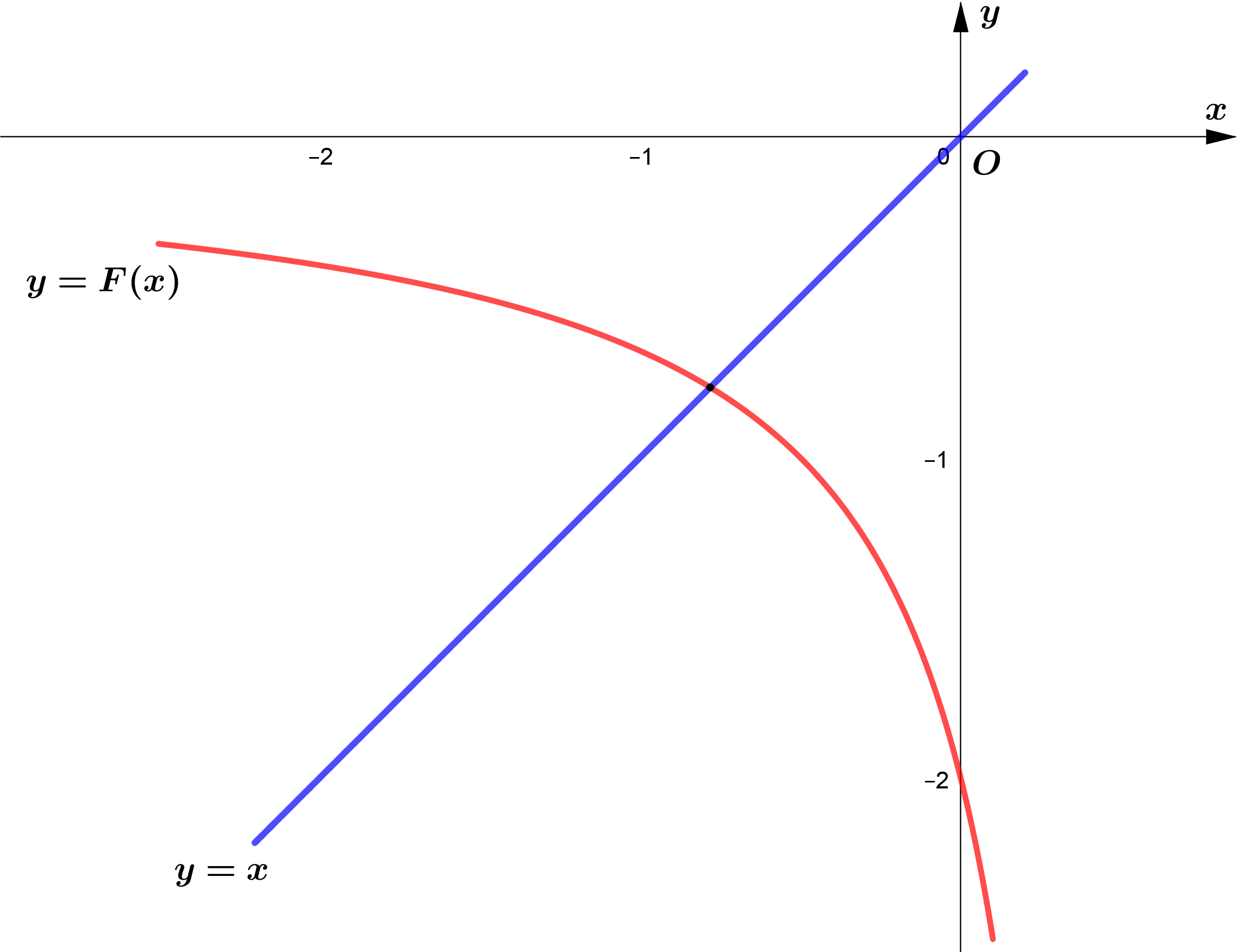
Graph အရ ဖြတ်မှတ်သည် $x=-2$ နှင့် $x=0$ ကြားတွင် ရှိသည်။ သို့သော်လက်တွေ့တွင် မည်သည့်နေရာ၌ ဖြတ်သည်ကို ကြိုတင် သိရှိခြင်းမရှိသောကြောင့် $x=0$ တွင် graph နှစ်ခု ဖြတ်သွားသည်ဟု ခန့်မှန်းပါမည်။ $x=0$ တွင် graph နှစ်ခု အမှန်တကယ် ဖြတ်သွား လျှင် $F(0)=0$ ဖြစ်မည်ပါမည်။
$F(0)=\dfrac{1}{0-\frac{1}{2}}=-2$
ထို့ကြောင့် $x\ne F(x)$ ဖြစ်သောကြောင့် $x=0$ တွင် graph နှစ်ခု မဖြတ်ကြောင်းသိနိုင်ပြီး $x=0$ သည် ပေထားသော ညီမျှခြင်း၏ solution မဟုတ်ကြောင်း သိနိုင်သည်။
$F(0)=-2$ မှ ရရှိသော $-2$ ကို root အဖြစ်ယူဆပြီး ဆက်၍ ရှာကြည့်ပါမည်။
$F(-2)=\dfrac{1}{-2-\frac{1}{2}}=-0.4, F(-2)\ne-2$ ဖြစ်သည်။ ထို့ကြောင့် $x=-2$ သည် ပေထားသော
ညီမျှခြင်း၏ solution မဟုတ်ပါ။
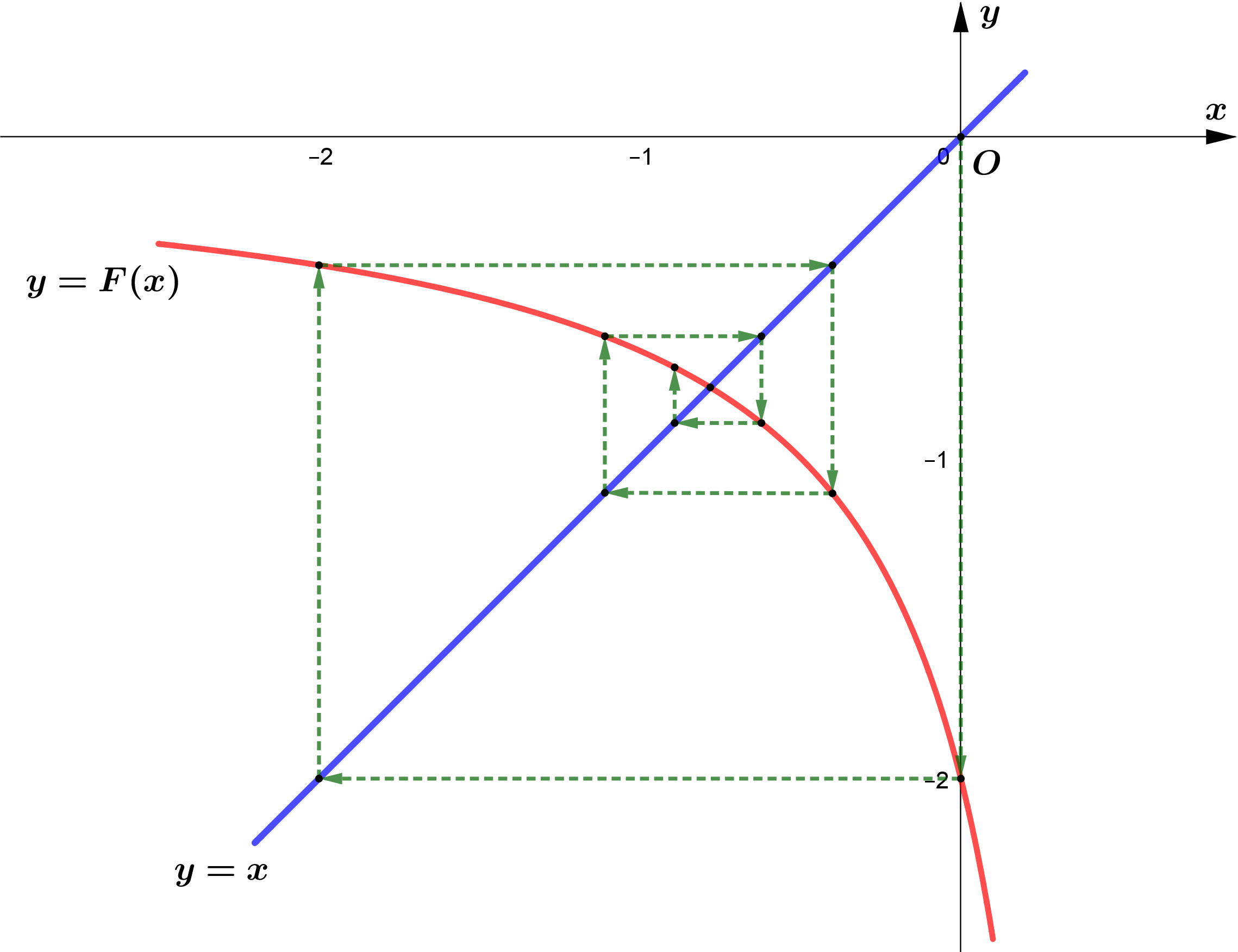
အထက်ပါနည်းအတိုင်း ရရှိလာသော $F(x)$ ကို $x_{\text{new}}$ ဟုယူဆပြီး တန်ဖိုးများကို ဆက်လက်ရှာကြည့်ပါမည်။
|
|
|---|
$x=F(x)$ ဖြစ်ရမည်ဟု မူလကသတ်မှတ်ခဲ့သည်ဖြစ်ရာ ဇယားပါ အချက်အလက်များအရ $x=-0.78$(two decimal places) သည် ပေးထားသော ညီမျှခြင်း၏ root ဖြစ်သည်ဟု သိရှိနိုင်ပါသည်။
အဆိုပါအခြေအနေကို $x=F(x)$ သည် converge ဖြစ်သည်ဟု ခေါ်သည်။
မူလပေးထားသော ညီမျှခြင်း $2x^2-x-2=0, x< 0$ ကို quadratic formula ဖြင့် ပြန်၍ check လုပ်ကြည့်လျှင်...
| $\begin{aligned} &\\ x&=\frac{-(-1)-\sqrt{(-1)^2-4(2)(-2)}}{2(2)}\\\\ &=-0.78\ (\text{two decimal places}), (\quad\because x < 0)\\\\ \end{aligned}$ |
|---|
အထက်ပါအတိုင်း ညီမျှခြင်းတစ်ခု၏ root ကို numerical merthod ဖြင့် ရှာယူနိုင်သည်။ ဖော်ပြခဲ့သော နည်းလမ်းကို iterative method ဟုခေါ်သည်။ Iterative method ကို အသုံးပြုပြီး အဖြေရှာခြင်း process ကို Iteration ဟုခေါ်သည်။ Iteration ကို Engineering, Computer Programming, Business စသော နယ်ပယ်များတွင် အသုံးချသည်။
Iterative Method
When trying to solve $f(x)$, rearrange the equation to the form $x=F(x)$. When $\alpha$ is the value of $x$ such that $x=F(x)$ then $\alpha$ is also a solution of $f(x)=0$.
Iterative Formula
$$\begin{array}{|c|} \hline x_{n+1}=F(x_n)\\ \hline \end{array}$$Question (1)
$f(x)=x^{2}-6 x+2$.
(a) Show that $f(x)=0$ can be written as $x=6-\dfrac{2}{x}$.
(b) Starting with $x=4$, use iterative formula to find a root of the
equation $f(x)=0$. Round your answers to 3 decimal places.
(c) Use the quadratic formula to find the roots to the equation $f(x)=0$,
leaving your answer in the form $a \pm \sqrt{b}$,
where $a$ and $b$ are constants to be found.
Question (2)
$f(x)=x^{2}-6 x+1$.
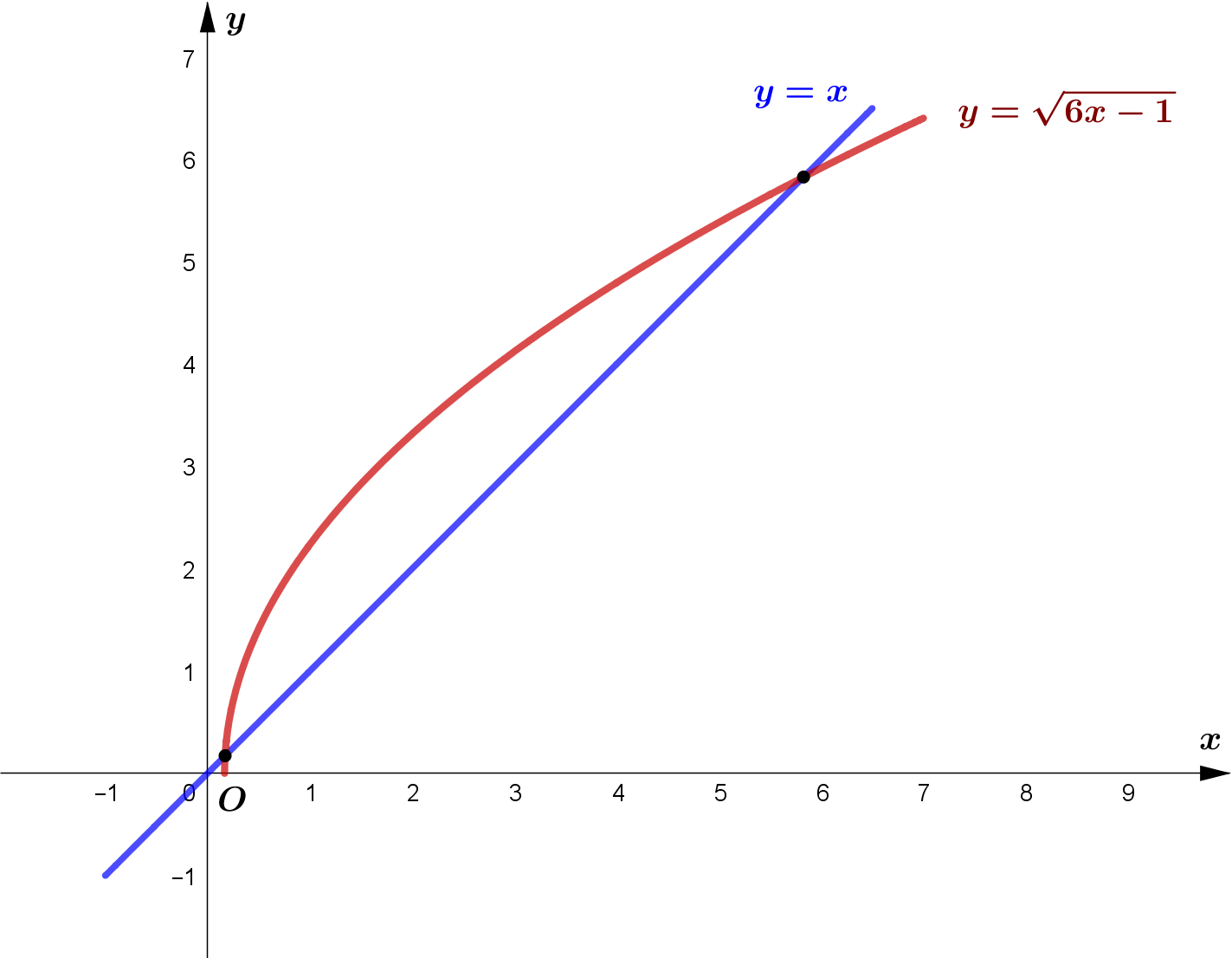
(a) Show that the equation $f(x)=0$ can be written as $x=\sqrt{6 x-1}$.
(b) Sketch on the same axes the graphs of $y=x$ and $y=\sqrt{6 x-1}$.
(c) Write down the number of roots of $f(x)$.
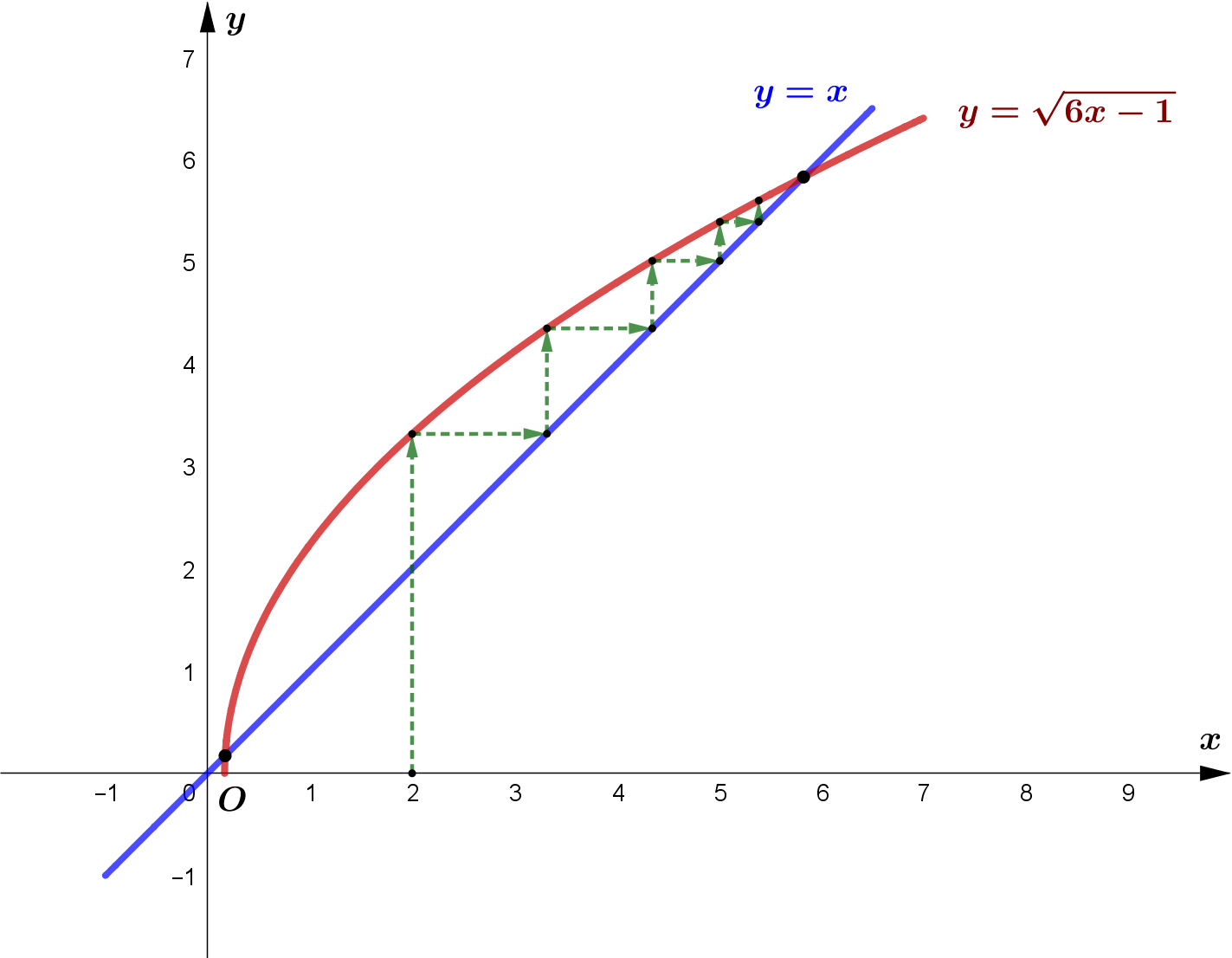
(d) Use your diagram to explain why the iterative formula $x=\sqrt{6 x-1}$
converges to a root of $f(x)$ when $x_{0}=2$.
Question (3)
The equation $e^{x}-1=2 x$ has a root $\alpha=0$.
(a) Show by calculation that this equation also has a root, $\beta$,
such that $1 <\beta < 2$.
(b) Show that this equation can be rearranged as $x=\ln (2 x+1)$.
(c) Use an iteration process based on the equation in part (b),
with a suitable starting value, to find $\beta$ correct to 3 significant
figures. Give the result of each step of the process to 5 significant figures.
Question (4)
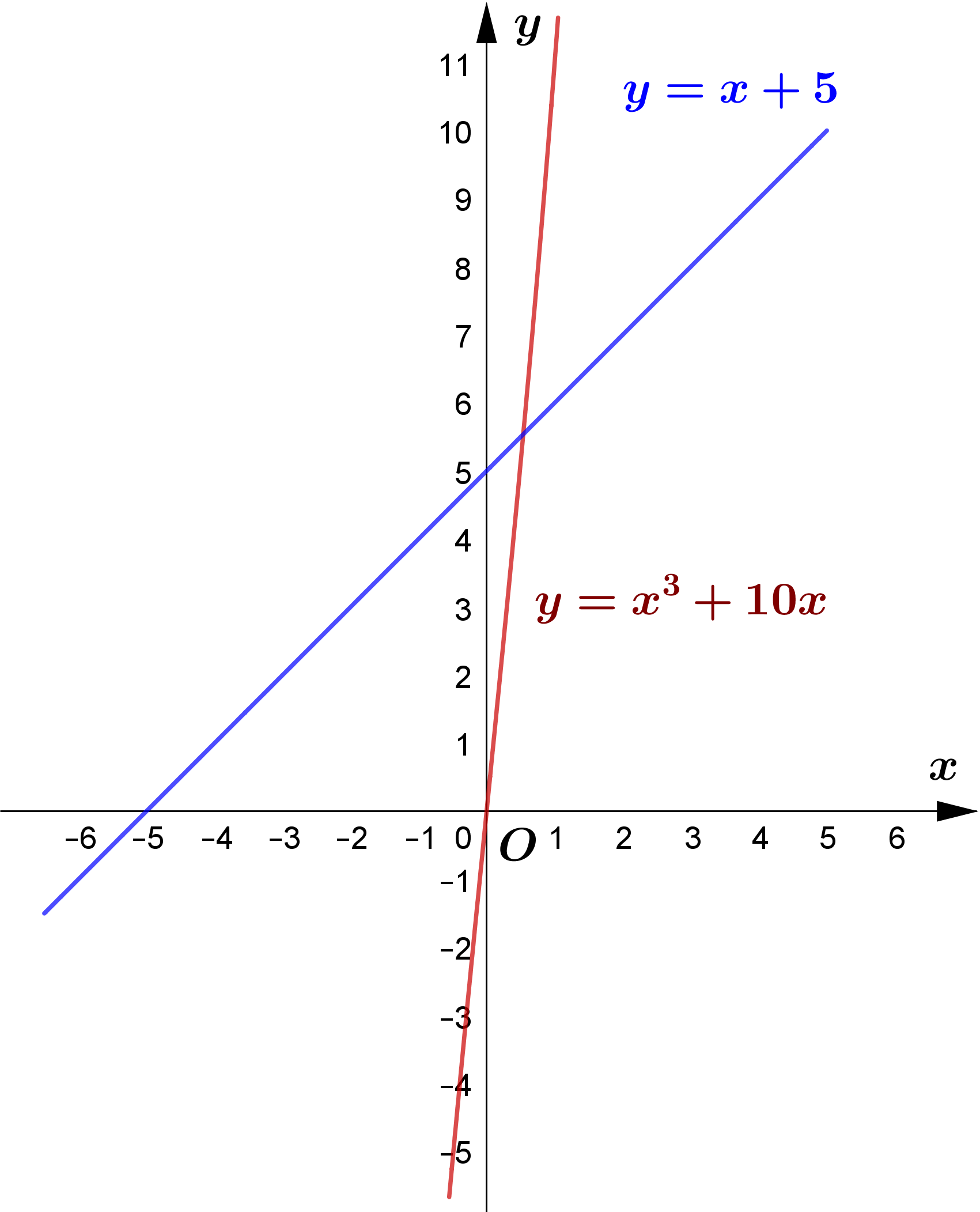
(a) By sketching a suitable pair of graphs, show that the equation
$x^{3}+10 x=x+5$ has only one root that lies between 0 and $1 .$
(b) Use the iterative formula $x_{n+1}=\dfrac{5-x_{n}^{3}}{9}$,
with a suitable value for $x_{1}$, to find the value of this
root correct to 4 decimal places. Give the result of each iteration
to 6 decimal places.
Question (5)
The terms of a sequence, defined by the iterative formula
$x_{n+1}=\ln \left(x_{n}^{2}+4\right)$, converge to the value $\alpha$.
The first term of the sequence is $2$ .
(a) Find the value of $\alpha$ correct to $2$ decimal places.
Give each term of the sequence you find to $4$ decimal places.
(b) The value $\alpha$ is a root of an equation of the form $x^{2}=f(x)$.
Find this equation.