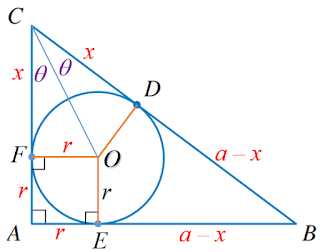
Problem Study (Geometry applying Trigonometry and Calculus)

(a) Let be a triangle with right angle and hypotenuse a=BC

.
(See the figure.)
If the inscribed circle touches the hypotenuse at D,
show that $CD = \frac{1}{2}\left( {BC + AC-AB} \right)$ .

(b) If $\theta = \frac{1}{2}\angle C$ , express the radius $r$ of the inscribed circle in terms of $a$ and $\theta$ .
(c) If $a$ is fixed and $\theta$ varies, find the maximum value of $r$ .
Solution
    Let $O$ be the centre of the circle and $E$ and $F$ be points of
    tangency of $AC$ and $AB$ respectively.
   BC = a

(given)
Draw

and

.
   $\therefore OE = OF = r$
   Since $OE \bot AB$ and $OF \bot AC$ , AEOF

is a square.

Therefore

Let

.
$\therefore \ BD = BE = a-x.$
(a)    $\frac{1}{2}\left( {BC + AC-AB} \right)$
      $=\frac{1}{2}(a + x + r-(r + a-x))$
      $=\frac{1}{2} \ (a + x + r -r - a + x)$
    = x

      $\therefore \ \ CD = \frac{1}{2}\left( {BC + AC-AB} \right).$
(b)   Draw

. Since $O$ is incentre,

bisects $\angle C$ .
        In right $\Delta \ COF$ , $\frac{x}{r}=\cot\theta$
   $\therefore \ x=r\cot\theta$

In right $\Delta \ ABC$ , By Pythagoras Theorem,
AB^2+AC^2=BC^2

       $\therefore \ (r+a-x)^2+(r+x)^2=a^2$
       $\therefore \ (r-x+a)^2+(r+x)^2=a^2$
      $\therefore \ (r-x)^2+2a(r-x)+a^2+(r+x)^2=a^2$
$\therefore \ (r-x)^2+2a(r-x)+(r+x)^2=0$
$\therefore \ (r-x)^2+(r+x)^2=2a(x-r)$
      $\therefore \ r^2-2xr+x^2+r^2+2xr+x^2 = 2a(x-r)$
$\therefore \ 2(r^2+x^2) = 2a(x-r)$
$\therefore \ (r^2+x^2) = a(x-r)$
    $\therefore \ (r^2+r^2\cot^2\theta ) = a(r\cot\theta-r)$
$\therefore \ r^2(1+\cot^2\theta ) = ar(\cot\theta-1)$
$\therefore \ r\csc^2\theta = a\left ( \frac{\cos\theta}{\sin\theta} -1\right )$
    $\therefore \ \frac{r}{\sin^2\theta} = a\left ( \frac{\cos\theta-\sin\theta}{\sin\theta} \right )$
$\therefore \ r=a(\sin\theta\cos\theta-\sin^2\theta)$
    $\therefore \ r=\frac{a}{2}(2\sin\theta\cos\theta-2\sin^2\theta)$
    $\therefore \ r=\frac{a}{2}(\sin2\theta-2\sin^2\theta)$
(c)   Since $a$ is fixed and $\theta$ varies,

is a function of $\theta$ and the rate of
change of

with respect to $\theta$ is
   $\frac{dr}{d\theta}=\frac{a}{2}(2\cos2\theta-4\sin\theta\cos\theta)$
    $\therefore \ \frac{dr}{d\theta}=a(\cos2\theta-\sin2\theta)$

has stationary value when $\frac{dr}{d\theta}=0$ .
    $\therefore \ a(\cos2\theta-\sin2\theta)=0$
$\therefore \ \cos2\theta=\sin2\theta$
$\therefore \ \tan2\theta=1$
    $\therefore \ 2\theta=\frac{ \pi}{4}$ and $\theta=\frac{ \pi}{8}$ .
      $\frac{d^2r}{d\theta^2}=a(-2\sin2\theta-2\cos2\theta)$
           $=-2a(\sin2\theta+\cos2\theta)$
      When $\theta=\frac{ \pi}{8}$ ,
$\frac{d^2r}{d\theta^2}=-2a\left ( \sin\frac{\pi }{4}+\cos\frac{\pi }{4} \right )=-2\sqrt 2 a<0$ .

will be maximum value when $\theta=\frac{ \pi}{8}$ .
      $\sin\frac{\pi}{8}=\sin\frac{\frac{\pi}{4}}{2}$
          $=\ \sqrt\frac{1-\cos\frac{\pi}{4}}{2}$
$=\ \sqrt\frac{1-\frac{\sqrt2}{2}}{2}$
    $=\ \frac{{\sqrt {2 - \sqrt 2 } }}{2}$
   $\therefore \ \sin^2\frac{\pi}{8}= \frac{{2 - \sqrt 2 }}{4}$
   $r=\frac{a}{2}(\sin2\theta-2\sin^2\theta)$
   $=\frac{a}{2}(\sin\frac{\pi}{4}-2\sin^2\frac{\pi}{8})$
   $=\frac{a}{2}\left (\frac{\sqrt2}{2}-2\left (\frac{2-\sqrt2}{4} \right ) \right )$
   $=\frac{a}{2}\left (\frac{\sqrt2}{2}-\frac{2-\sqrt2}{2} \right )$
   $=\frac{a}{2}\left (\sqrt2-1\right )$ $\Leftarrow$

စာဖတ်သူ၏ အမြင်ကို လေးစားစွာစောင့်မျှော်လျက်!

Problem Study (Geometry applying Trigonometry and Calculus)

Contact Form