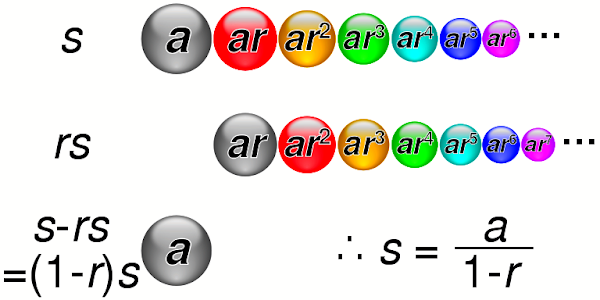Infinite Sum of Geometric Series : Part (1)

Infinite Geometric Series

A geometric series with infinite number of terms is called an infinite geometric series.

Geometric Progression တစ်ခု၏ $n$ terms အထိ ပေါင်းလဒ်ကို

$S_n= \dfrac{a(1-r^n)}{1-r}$

ဟုသိရှိခဲ့ပြီး ဖြစ်သည်။ ညီမျှခြင်းကို အောက်ပါအတိုင်း အကျယ်ဖြန့်ကြည့်ပါမည်။

$\begin{aligned} S_n&= \dfrac{a(1-r^n)}{1-r}\\\\ &= \dfrac{a-ar^n}{1-r}\\\\ &= \dfrac{a}{1-r}-\dfrac{ar^n}{1-r}\\\\ \end{aligned}$

Case I.
$|r|>1 \text{ i.e., } r<-1 \text{ or } r>1,$
$(\text{ e.g., } a=2, r=2)$

$\begin{aligned} S_n &= \dfrac{2}{1-2}-\dfrac{2\times2^n}{1-2}\\\\ &= -2+2\times2^n\\\\ &= 2(2^n - 1)\\\\ \end{aligned}$ $\begin{array}{|r|r|} \hline n\hspace{.2cm} & S_n\hspace{4cm} \\ \hline 1 & 2 \\ \hline 5 & 62 \\ \hline 10 & 2046 \\ \hline 50 & 2251799813685246 \\ \hline 100 & 2535301200456458802993406410750 \\ \hline \end{array}$

ထိုအခါ $n$ ၏ တန်ဖိုးကြီးလာသည်နှင့် အမျှ $S_n$ ၏ ပမာဏ (magnitude) သည်လည်း ကြီးလာပါမည်။

$n\rightarrow \infty$ ($n$ သည် အနန္တပမာဏသို့ ချဉ်းကပ်သွားသည်)

$S_n\rightarrow \infty$ ($S_n$ သည်လည်း အနန္တပမာဏသို့ ချဉ်းကပ်သွားသည်)

ထို့ကြောင့် အနန္တကိန်းလုံးအရေအတွက်ထိ ပေါင်းလဒ်ကို ရှာယူရန် မဖြစ်နိုင်တော့ပါ။

ထိုအခြေအနေကို divergent condition ဟုခေါ်သည်။ Divergent Condition တွင် Infinite Sum (အနန္တကိန်းလုံးအရေအတွက်ထိ ပေါင်းလဒ်) ကို ရှာ၍မရနိုင်ပါ။

Key Point

If $|r|>1$, the geometric series is divergent, and Sum to Infinity doesn't exist.

Case II.
$|r|=1 \text{ i.e., } r=\pm 1$

အကယ်၍ $r=1$ ဖြစ်လျှင်

$S_n = a + a + a + \dots$ to $n$ terms = $na$

ထိုအခါ $n$ ၏ တန်ဖိုးကြီးလာသည်နှင့် အမျှ $S_n$ ၏ ပမာဏ (magnitude) သည်လည်း ကြီးလာပါဦးမည်။

ထို့ကြောင့် အနန္တကိန်းလုံးအရေအတွက်ထိ ပေါင်းလဒ်ကို ရှာယူရန် မဖြစ်နိုင်တော့ပါ။

အကယ်၍ $r=-1$ ဖြစ်လျှင်

$S_n = a - a + a -a + a - \dots$ to $n$ terms = $a \text { if } n \text { is odd}$

$S_n = a - a + a -a + a - \dots$ to $n$ terms = $0 \text { if } n \text { is even}$

ထို့ကြောင့် အနန္တကိန်းလုံးအရေအတွက်ထိ ပေါင်းလဒ်ကို ရှာယူရန် မလိုတော့ပါ။

Key Point

If $|r|=1$,the geometric series is also a type of divergent series and Sum to Infinity doesn't exist.

Case III.
$|r|<1 \text{ i.e., } -1< r < 1 $
$ (\text{ e.g., } a=2, r=\dfrac{1}{2})$

$\begin{aligned} S_n &= \dfrac{2}{1-1/2}-\dfrac{2\times(1/2)^n}{1-1/2}\\\\ &= 4-4{\left( {\dfrac{1}{2}} \right)}^{n}\\\\ &= 4\left[ {1-{{{\left( {\dfrac{1}{2}} \right)}}^{n}}} \right]\\\\ \end{aligned}$ $\begin{array}{|r|l|r|} \hline n\hspace{.2cm} & \hspace{1.5cm}r^n & S_n\hspace{2.5cm} \\ \hline 1 & 0.5 & 2 \\ \hline 2 & 0.25 & 3 \\ \hline 3 & 0.125 & 3.5 \\ \hline 4 & 0.0525 & 3.75 \\ \hline 5 & 0.03125 & 3.875 \\ \hline 10 & 0.0009765625 & 3.9960937500000000000 \\ \hline 50 & 8.88\times 10^{-16}\approx 0 & 3.9999999999999964473 \\ \hline 100 & 7.88\times 10^{-31}\approx 0 & 4.0000000000000000000 \\ \hline 1000 & 9.33\times 10^{-32}\approx 0 & 4.0000000000000000000 \\ \hline \end{array}$

ထိုအခါ $n$ ၏ တန်ဖိုးကြီးလာသည်နှင့် အမျှ $S_n$ ၏ ပမာဏ (magnitude) သည် တန်ဖိုးတစ်ခုတွင် မပြောင်းလဲတော့ဘဲ ကိန်းသေ ဖြစ်လာပါသည်။

$|r|< 1$ အတွက် $n\rightarrow \infty$ ဖြစ်သည့်အခါ $S_n$ သည် တန်ဖိုးတစ်ခုတွင် မပြောင်းမလဲ တည်ရှိနေသည်။ အဆိုပါတန်ဖိုးမှာ limit of $S_n$ as $n$ approaches $\infty$ ပင် ဖြစ်သည်။

$\begin{aligned} \lim _{n \rightarrow \infty} S_{n} &=\lim _{n \rightarrow \infty}\left(\dfrac{a}{1-r}-\dfrac{a r^{n}}{1-r}\right) \\ &=\dfrac{a}{1-r} \times \lim _{n \rightarrow \infty}\left(1-r^{n}\right) \\ &=\dfrac{a}{1-r}(1-0) \quad(\because\ |r|<1)\\ &=\dfrac{a}{1-r} \end{aligned}$

အထက်ဖေါ်ပြပါ geometric series အမျိုးအစားကို convergent series ဟုခေါ်ပြီး Converget Geometric Series တစ်ခုတွင် infinite sum (Sum to infinity) ရှိသည်ဟု မှတ်ယူရမည်။ Sum to Infinity ကို သင်္ကေတအားဖြင့် $(S)$ ဟုသတ်မှတ်သည်။

Key Point

If $|r|<1$,the geometric series is convergent series and Sum to Infinity exists. The sum to infinity of a convergent geometric series is denoted by $S$.

$\begin{array}{|l|} \hline S=\dfrac{a}{1-r}\\ \hline \end{array}$

Exercises

1. Determine whether the sum to infinity for each of the following geometric progression exist and find the sum to infinity where they exist.
   $\begin{aligned} &\\ \text{(a)} &\ 3,0.3,0.03, \ldots \\\\ \text{(b)} &\ \dfrac{1}{2}, \dfrac{2}{3}, \dfrac{8}{7}, \dfrac{32}{27}, \ldots \\\\ \text{(c)} &\ \dfrac{7}{2}, 3, \dfrac{18}{7}, \dfrac{108}{49}, \ldots\\\\ \end{aligned}$
   
   
   

   (a) $3,0.3,0.03, \ldots$ is a G.P. $\begin{aligned} &\\ \therefore\ a &=3 \\\\ r &=\dfrac{0.3}{3}=\dfrac{1}{10} \\\\ |r| &=\dfrac{1}{10}< 1\\\\ \end{aligned}$ $\therefore$ Sum to infinity exists. $\begin{aligned} &\\ S &=\dfrac{a}{1-r} \\\\ &=\dfrac{3}{1-\dfrac{1}{10}} \\\\ &=\dfrac{10}{3}\\\\ \end{aligned}$ (b) $\dfrac{1}{2}, \dfrac{2}{3}, \dfrac{8}{9}, \dfrac{32}{27}, \ldots$ is a G.P. $\begin{array}{l} \\ a=\dfrac{1}{2} \\\\ r=\dfrac{2 / 3}{1 / 2}=\dfrac{4}{3} \\\\ \therefore\ |r|=\dfrac{4}{3}>1\\\\ \end{array}$ $\therefore$ Sum to infinity doesn't exist. $\dfrac{7}{2}, 3, \dfrac{18}{7}, \dfrac{108}{49}, \ldots$ is a G.P. $\begin{array}{l} \\ a=\dfrac{7}{2} \\\\ r=\dfrac{3}{(7 / 2)}=\dfrac{6}{7} \\\\ |r|=\dfrac{6}{7}<1\\\ \end{array}$ $\therefore$ Sum to infinity exists. $\begin{aligned} &\\ S &=\dfrac{a}{1-r} \\\\ &=\dfrac{7 / 2}{1-\dfrac{6}{7}} \\\\ &=\dfrac{7}{2} \times 7 \\\\ &=\dfrac{49}{2} \end{aligned}$

   
   
   
2. Find the sum to infinity of the following geometric series.
   $\begin{aligned} &\\ \text{(a)} &\ 2+\dfrac{4}{3}+\dfrac{8}{9}+\ldots\\\\ \text{(b)} &\ 2+\dfrac{1}{2}+\dfrac{1}{8}+\dfrac{1}{32} \ldots\\\\ \text{(c)} &\ 3-\dfrac{2}{3}+\dfrac{4}{27}+\ldots\\\\ \text{(d)} &\ 81-27+9-3+\ldots\\\\ \end{aligned}$
   
   
   

   \begin{aligned} \text{(a) }\quad 2 &+\dfrac{4}{3}+\dfrac{8}{9}+\cdots \\\\ a &=2 \\\\ r &=\dfrac{4 / 3}{2}=\dfrac{2}{3} \\\\ S &=\dfrac{a}{1-r} \\\\ &=\dfrac{2}{1-\dfrac{2}{3}} \\\\ &=\dfrac{2}{1 / 3} \\\\ &=6 \end{aligned} $\begin{aligned} \text { (b) }\quad 2 &+\dfrac{1}{2}+\dfrac{1}{8}+\dfrac{1}{32}+\cdots \\\\ a &=2 \\\\ r &=\dfrac{1 / 2}{2}=\dfrac{1}{4} \\\\ S &=\dfrac{a}{1-r} \\\\ &=\dfrac{2}{1-\dfrac{1}{4}} \\\\ &=2 \times \dfrac{4}{3} \\\\ &=\dfrac{8}{3} \end{aligned}$ $\begin{aligned} &\\\\ \text { (c) }\quad &3 -\dfrac{2}{3}+\dfrac{4}{27}-\cdots \\\\ a &=3 \\\\ r &=\dfrac{-2 / 3}{3}=-\dfrac{2}{9} \\\\ S &=\dfrac{a}{1-r} \\\\ &=\dfrac{3}{1+\dfrac{2}{9}} \\\\ &=3 \times \dfrac{9}{11} \\\\ &=\dfrac{27}{11} \end{aligned}$ $\begin{aligned} &\\\\ \text { (d) }\quad &81 -27+9-3+\cdots \\\\ a &=81 \\\\ r &=-\dfrac{27}{81}=-\dfrac{1}{3} \\\\ S &=\dfrac{a}{1-r} \\\\ &=\dfrac{81}{1+\dfrac{1}{3}} \\\\ &=81 \times \dfrac{3}{4} \\\\ &=\dfrac{243}{4} \end{aligned}$

   
   
   
3. The $3^{\text {rd }}$ and $6^{\text {th }}$ term of a geometric progression are $9$ and $2 \dfrac{2}{3}$ respectively. Calculate the common ratio, the first term and the sum to infinity of the progression.
   
   
   
   

   $\begin{aligned} \text { In a G.P., }&\\\\ u_{3}&=9 \\\\ a r^{2}&=9 \ldots(1)\\\\ u_{6}&=2 \dfrac{2}{3}\\\\ a r^{5}&=\dfrac{8}{3} \cdots(2) \\\\ \text{B y } (2) \div(1)& \\\\ \dfrac{a r^{5}}{a r^{2}}&=\dfrac{8 / 3}{9}\\\\ r^{3}&=\dfrac{8}{27} \\\\ r&=\dfrac{2}{3}\\\\ \text { Substitute } r&=\dfrac{2}{3} \text { in equation }(1), \\\\ a\left(\dfrac{2}{3}\right)^{2}&=9 \\\\ a&=\dfrac{81}{4} \\\\ S&=\dfrac{a}{1-r} \\\\ & =\dfrac{81 / 4}{1-\dfrac{2}{3}} \\\\ & =\dfrac{81}{4} \times 3 \\\\ & =\dfrac{243}{4} \end{aligned}$

   
   
   
4. The sum of an infinite geometric progression is $12$ and its first term is $3$ . Fin the first four terms of the G.P.
   
   
   
   

   $\begin{aligned} \text { In a G.P., } & \\\\ S=12, a&=3 \\\\ \therefore\ \dfrac{3}{1-r}&=12 \\\\ 1-r&=\dfrac{1}{4} \\\\ r&=\dfrac{3}{4} \\\\ \therefore u_{1}=a&=3 \\\\ u_{2}=a r&=\dfrac{9}{4} \\\\ u_{3}=a r^{2}&=\dfrac{27}{16} \\\\ u_{4}=a r^{3}&=\dfrac{81}{64} \end{aligned}$

   
   
   
5. In a G.P. the ratio of the sum of the first three terms to the sum to infinity is $19: 27$. Find the common ratio.
   
   
   
   

   Let the first term be $a$ and the common ratio be $r$ for the given G.P. By the problem, $\begin{aligned} &\\ \dfrac{S_{3}}{S}&=\dfrac{19}{27} \\\\ \dfrac{\dfrac{a\left(1-r^{3}\right)}{1-r}}{\dfrac{a}{1-r}}&=\dfrac{19}{27} \\\\ 1-r^{3}&=\dfrac{19}{27} \\\\ r^{3}&=\dfrac{8}{27}\\\\ \therefore r&=\dfrac{2}{3} \end{aligned}$

   
   
   
6. The second term of a G.P. is $2$ and its sum to infinity is $9$ . Find the sum of the first $4$ terms of the two possible geometric progressions.
   
   
   
   

   $\begin{aligned} \text { In a G.P., }\quad & \\\\ u_{2}&=2 \\\\ a r&=2 \\\\ a&=\dfrac{2}{r} \\\\ S&=9 \\\\ \dfrac{a}{1-r}&= 9 \\\\ \dfrac{\dfrac{2}{r}}{1-r}&=9 \\\\ \dfrac{2}{r}&=9-9 r \\\\ 9 r^{2}-9 r+2&=0\\\\ (3 r-1)(3 r-2)&=0 \\\\ r=\dfrac{1}{3} & \text { or } r=\dfrac{2}{3} \\\\ \end{aligned}$ $\begin{aligned} \text { When } r&=\dfrac{1}{3}, \\\\ a&=\dfrac{2}{1 / 3}=6 \\\\ \therefore S_4&=\dfrac{a(1-r^4)}{1-r} \\\\ & = \dfrac{6 (1-(1/3)^4)}{1-1/3}\\\\ & = \dfrac{6 (1-\dfrac{1}{81})}{\dfrac{2}{3}}\\\\ & = \dfrac{6 \times\dfrac{80}{81}}{\dfrac{2}{3}}\\\\ &=\dfrac{80}{9}\\\\ \text { When } r&=\dfrac{2}{3}, \\\\ a&=\dfrac{2}{2 / 3}=3 \\\\ \therefore S_4&=\dfrac{a(1-r^4)}{1-r} \\\\ & = \dfrac{3(1-(2/3)^4)}{1-2/3}\\\\ & = \dfrac{3 (1-\dfrac{16}{81})}{\dfrac{1}{3}}\\\\ & = \dfrac{3 \times\dfrac{65}{81}}{\dfrac{1}{3}}\\\\ &=\dfrac{65}{9} \end{aligned}$

   
   
   
7. The sum of the first 3 terms of a G.P. is $27$ and the sum of the fourth, fifth and sixth terms is $-1$. Find the common ratio and the sum to infinity of the G.P.
   
   
   
   

   $\begin{aligned} \text { In a G.P., }& \\\\ u_{1}+u_{2}+u_{3}&=27 \\\\ a+a r+a r^{2}&=27 \ldots(1) \\\\ u_{4}+u_{5}+u_{6}&=-1 \\\\ a r^{3}+a r^{4}+a r^{5}&=-1 \cdots(2) \\\\ \text {By }(2) \div(1),& \\\\ \dfrac{a r^{3}+a r^{4}+a r^{5}}{a+a r+a r^{2}}&=-\dfrac{1}{27} \\\\ \dfrac{r^{3}\left(a+a r+a r^{2}\right)}{\left(a+a r+a r^{2}\right)}&=-\dfrac{1}{27} \\\\ \therefore\ r^{3}&=-\dfrac{1}{27}\\\\ r&=-\dfrac{1}{3}\\\\ \end{aligned}$ $\begin{aligned} &\text{Substitue } r=-\dfrac{1}{3} \text{ in equation } (1),\\\\ &a+a \left(-\dfrac{1}{3}\right) +a \left(-\dfrac{1}{3}\right)^2 =27 \\\\ &a - \dfrac{a}{3} + \dfrac{a}{9} = 27\\\\ &\dfrac{7a}{9}= 27\\\\ &a=\dfrac{243}{7}\\\\ \end{aligned}$ $\begin{aligned} S&=\dfrac{a}{1-r}\\\\ &=\dfrac{\dfrac{243}{7}}{1+\dfrac{1}{3}}\\\\ &=\dfrac{729}{28} \end{aligned}$

   
   
   
8. Given that $x+18, x+4$ and $x-8$ are the first three terms of a G.P., find the value of $x$. Hence find
   (a) the common ratio
   (b) the fifth term
   (c) the sum to infinity.
   
   
   
   

   $\begin{aligned} &x+18, x+4, x-8 \text { are in G.P. } \\\\ &\dfrac{x+4}{x+18}=\dfrac{x-8}{x+4} \\\\ &\therefore\ x^{2}+8 x+16 = x^{2}+10 x-144 \\\\ \end{aligned}$ $\begin{aligned} 2x &= 160 \\\\ x &=80 \\\\ \therefore\ u_{1}&=98 \\\\ u_{2}&= 84 \\\\ u_{3}&= 72 \\\\ \therefore\ a&=98 \\\\ r&=\dfrac{84}{98}\\\\ &=\dfrac{6}{7} \\\\ \end{aligned}$ $\begin{aligned} \therefore\ u_5 &= ar^4\\\\ &= 98 \times\left(\dfrac{6}{7}\right)^{4}\\\\ &=\dfrac{2592}{49}\\\\ S &= \dfrac{a}{1-r}\\\\ &= \dfrac{98}{1-\dfrac{6}{7}}\\\\ &=686 \end{aligned}$

   
   
   
9. Given that $2 x-14, x-4$ and $\dfrac{1}{2} x$ are successive terms of a sequence.
   (a) find the value of $x$ when the sequence is (i) an A.P. (ii) a G.P.
   (b) If $2 x-14$ is the $3^{\text {rd }}$ term of a G.P. with infinite terms, find
   (i) the common ratio
   (ii) the sum to infinity.
   
   
   
   

   $2 x-14, x-4, \dfrac{1}{2} x$ are successive terms of a sequence. When the sequence is an A.P., $\begin{aligned} &\\ x-4-(2 x-14)&=\dfrac{1}{2} x-(x-4) \\\\ -x+10&=-\dfrac{1}{2} x+4 \\\\ \dfrac{1}{2} x&=6 \\\\ x&=12\\\\ \end{aligned}$ When the sequence is G.P., $\begin{aligned} &\\ \dfrac{x-4}{2 x-14}&=\dfrac{\dfrac{1}{2} x}{x-4}\\\\ x^{2}-8 x+16&=x^{2}-7 x \\\\ \therefore\ x&=16 \\\\ u_{3}&=a r^{2}\\\\ &=2 x-4\\\\&=28 \\\\ u_{4}&=a r^{3}\\\\ &=x-4\\\\&=14 \\\\ \therefore\ r&=\dfrac{u_{4}}{u_{3}}\\\\ &=\dfrac{14}{28}\\\\ &=\dfrac{1}{2} \\\\ \therefore\ a\left(\dfrac{1}{2}\right)^{2}&=28 \\\\ S&=\dfrac{a}{1-r}\\\\ &=\dfrac{112}{1-\dfrac{1}{2}}\\\\ &=224 \end{aligned}$

   
   
   
10. A G.P. has a first term $18$ and a sum to infinity of $30$. Each of the terms in the progression is squared to form a new G.P. Find the sum to infinity of the new progression.
    
    
    
    

    Let the first termbe $a$ and the common ratio be $r$ for the given G.P. $\begin{aligned} &\\ a&=18 \\\\ S&=30 \\\\ \dfrac{a}{1-r}&=30 \\\\ \dfrac{18}{1-r}&=30 \\\\ 1-r&=\dfrac{3}{5} \\\\ \therefore\ r&=\dfrac{2}{5}\\\\ \end{aligned}$ Each tems of the progression is squared, the new sequence formed is $a^{2}, a^{2} r^{2}, a^{2} r^4, a^{2}r^6, \ldots\\\\ $ Let the first term be $A$ and the common ratio be $R$ for the new G.P., $\begin{aligned} &\\ \therefore A &=a^{2}=18^{2} \\\\ R &=\dfrac{a^{2} r^{2}}{a^{2}}\\\\ &=r^{2}\\\\ &=\dfrac{4}{25}\\\\ \end{aligned}$ Let the sum to infinity be $S$. $\begin{aligned} &\\ \therefore\ S &=\dfrac{A}{1-R} \\\\ &=\dfrac{18^{2}}{1-\dfrac{4}{25}} \\\\ &=\dfrac{2700}{7} \end{aligned}$

    
    
    
11. The first term of a G.P is $a$ and the common ratio is $r$. Given that $a+96 r=0$ and that the sum to infinity is $32$ , find the $8^{\text {th }}$ term.
    
    
    
    

    $\begin{aligned} a+96 r &=0 \\\\ a &=-96 r \\\\ s &=32 \\\\ \dfrac{a}{1-r} &=32 \\\\ \dfrac{-96 r}{1-r} &=32 \\\\ -96 r &=32-32 r \\\\ -64 r &=32 \\\\ r &=-\dfrac{1}{2} \\\\ a &=48 \\\\ 48 &=a r^{7} \\\\ &=48 \cdot\left(-\dfrac{1}{2}\right)^{7} \\\\ &=-\dfrac{3}{8} \end{aligned}$

    
    
    
12. An infinite geometric series has a finite sum of $256$ . The sum of the first $3$ terms is $224$. What is the value of the $3^{\text {rd }}$ term?
    
    
    
    

    $\begin{aligned} S&=256 \\\\ \dfrac{a}{1-r}&=256 \ldots(1) \\\\ S_{3}&=224 \\\\ \dfrac{a\left(1-r^{3}\right)}{1-r}&=224 \cdots(2) \\\\ \text{By } & (2) \div(1), \\\\ \dfrac{\dfrac{a\left(1-r^{3}\right)}{1-r}}{\dfrac{a}{1-r}}&=\dfrac{224}{256} \\ 1-r^{3}&=\dfrac{7}{8}\\\\ r^3&=\dfrac{1}{8}\\\\ r&=\dfrac{1}{2}\\\\ \text{Substitue }& r=\dfrac{1}{2} \text{ in equation (1).}\\\\ \dfrac{a}{1-\dfrac{1}{2}}&=256\\\\ a&=128\\\\ \therefore\ u_3&=ar^2=128\left(\dfrac{1}{2}\right)^2=32 \end{aligned}$

    
    
    
13. In a G.P., whose first term is positive, the sum of the first and third terms $\dfrac{13}{9}$ and the product of second and fourth terms is $\dfrac{16}{81}$. Find the common ratio and the sum to infinity.
    
    
    
    

    $\begin{aligned} &\text { In a G.P., } \\\\ &a>0 \\\\ &u_{1}+u_{3}=\dfrac{13}{9} \\\\ &a+ar^{2}=\dfrac{13}{9} \cdots(1) \\\\ &u_{2} \cdot u_{4}=\dfrac{16}{81} \\\\ &ar \cdot a r^{3}=\dfrac{16}{81} \\\\ &\left(a r^{2}\right)^{2}=\dfrac{16}{8}\\\\ &a r^{2}=\dfrac{4}{9} \quad(\because a>0) \quad \ldots(2)\\\\ \end{aligned}$ Substitue $a r^{2}=\dfrac{4}{9}$ in equation (1), $\begin{aligned} &\\ &a+\dfrac{4}{9}=\dfrac{13}{9} \\\\ &a=1\\\\ \end{aligned}$ Substitue $a=1$ in equation (2), $\begin{aligned} &\\ &r^{2}=\dfrac{4}{9} \\\\ &r=\pm \dfrac{2}{3}\\\\ \end{aligned}$ When $a=1, r=-\dfrac{2}{3}$ $\begin{aligned} &\\ S &=\dfrac{a}{1-r} \\\\ &=\dfrac{1}{1+\dfrac{2}{3}} \\\\ &=\dfrac{3}{5}\\\\ \end{aligned}$ When $a=1, r=\dfrac{2}{3}$ $\begin{aligned} &\\ S &=\dfrac{a}{1-r} \\\\ &=\dfrac{1}{1-\dfrac{2}{3}} \\\\ &=3 \end{aligned}$

    
    
    
14. In a G.P. the sum of the first term and the fourth term is $144$ , and the first term exceeds the seventh term by $126$ . Find the first term, the common ratio and the sum to infinity of the G.P.
    
    
    
    

    $\begin{aligned} &\text { In a G.P, } \\\\ &u_{1}+u_{4}=144 \\\\ &a+a r^{3}=144 \cdots(1) \\\\ &u_{1}-u_{7}=126 \\\\ &a-a r^{6}=126 \cdots(2) \\\\ &\text{By } (2) \div(1), \\\\ &\dfrac{a-a r^{6}}{a+a r^{3}}=\dfrac{126}{144}\\\\ &\dfrac{a\left(1-r^{6}\right)}{a\left(1+r^{3}\right)}=\dfrac{7}{8} \\\\ &\dfrac{\left(1+r^{3}\right)\left(1-r^{3}\right)}{1+r^{3}}=\dfrac{7}{8} \\\\ &1-r^{3}=\dfrac{7}{8} \\\\ &r^{3}=\dfrac{1}{8} \\\\ &r=\dfrac{1}{2}\\\\ \end{aligned}$ Substitue $r=\dfrac{1}{2}$ in equation (1). $\begin{aligned} &\\ a+\dfrac{a}{8}&=144\\\\ \dfrac{9 a}{8} &=144 \\\\ a &=128 \\\\ S &=\dfrac{a}{1-r} \\\\ &=\dfrac{128}{1-\dfrac{1}{2}} \\\\ &=256 \end{aligned}$

    
    
    
15. The first term of a G.P. is $3$ and the common ratio is $\dfrac{2}{5}$. Find the sum to infinity, and the least value of $n$ for which the sum to $n$ terms differ from the sum to infinity by less than $0.04$.
    
    
    
    

    $\begin{aligned} \text{In a G.P, } \\\\ a &=3, r=\dfrac{2}{5} \\\\ S &=\dfrac{a}{1-r} \\\\ &=\dfrac{3}{1-\dfrac{2}{5}} \\\\ &=5 \\\\ S_{n} &=\dfrac{a\left(1-r^{n}\right)}{1-r} \\\\ &=5\left[1-\left(\dfrac{2}{5}\right)^{n}\right]\\\\ \end{aligned}$ By the problem, $\begin{aligned} &\\ S-S_{n} & < 0.04 \\\\ 5-5\left[1-\left(\dfrac{2}{5}\right)^{n}\right] & < 0.04 \\\\ 5\left(\dfrac{2}{5}\right)^{n} & < 0.04 \\\\ \left(\dfrac{2}{5}\right)^{n} & <0.008 \\\\ \left(\dfrac{5}{2}\right)^{n} & <125 \\\\ (2.5)^{n} &>125\\\\ n&>\log _{2.5} 125\\\\ n&>\dfrac{\ln 125}{\ln 2.5}\\\\ n&>5.269\\\\ \end{aligned}$ $\therefore$ The least value of $n=6$.

    
    
    

စာဖတ်သူ၏ အမြင်ကို လေးစားစွာစောင့်မျှော်လျက်!