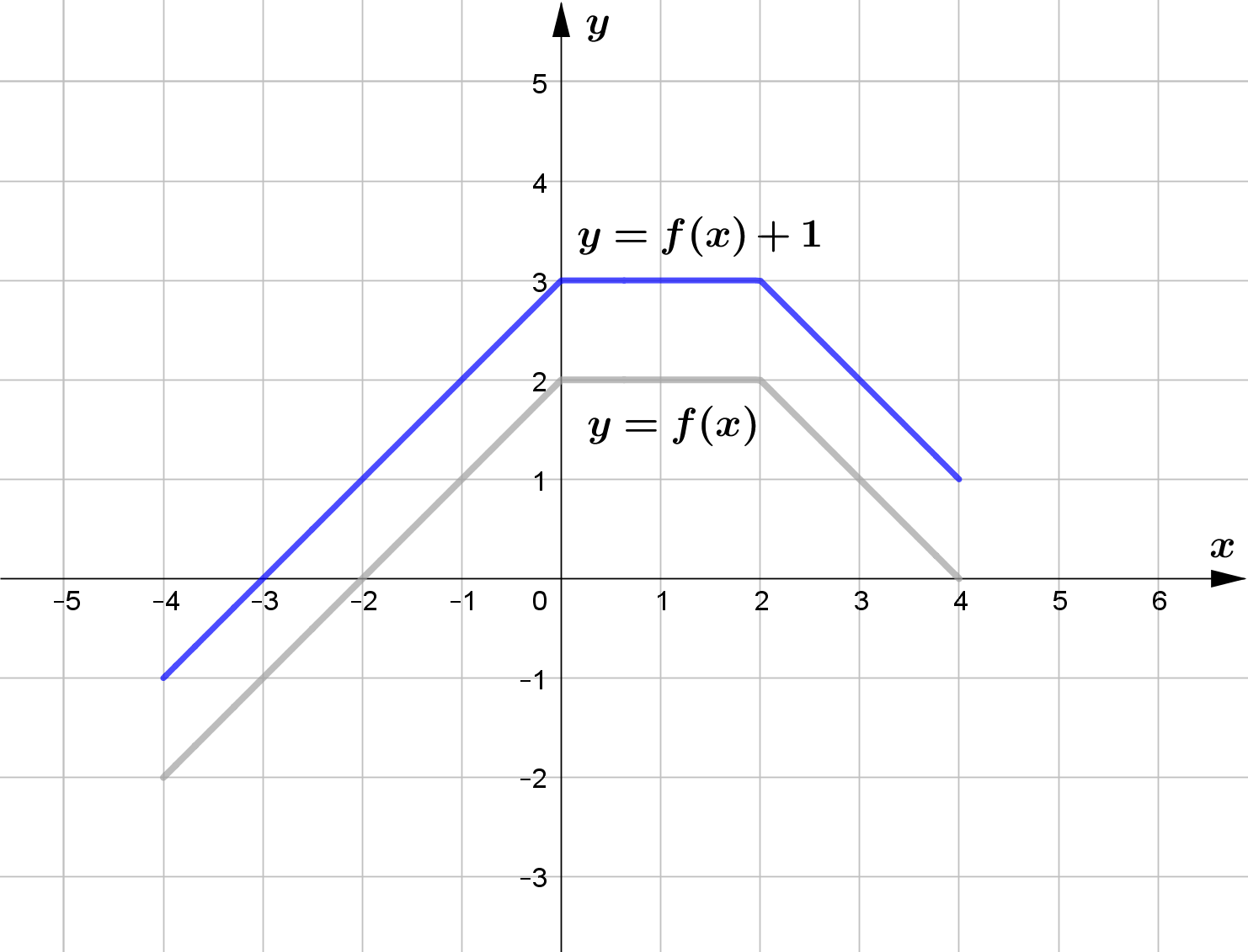
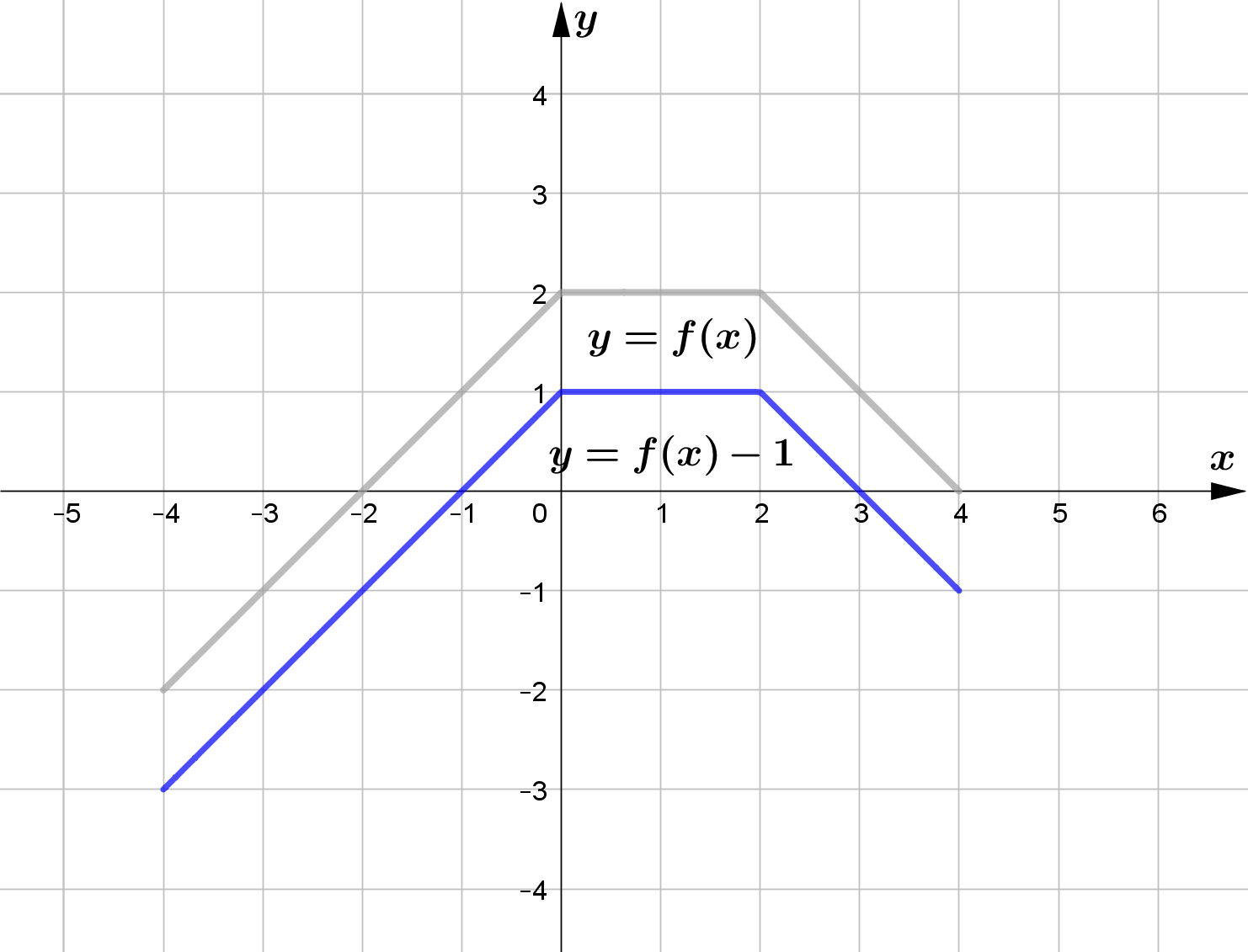
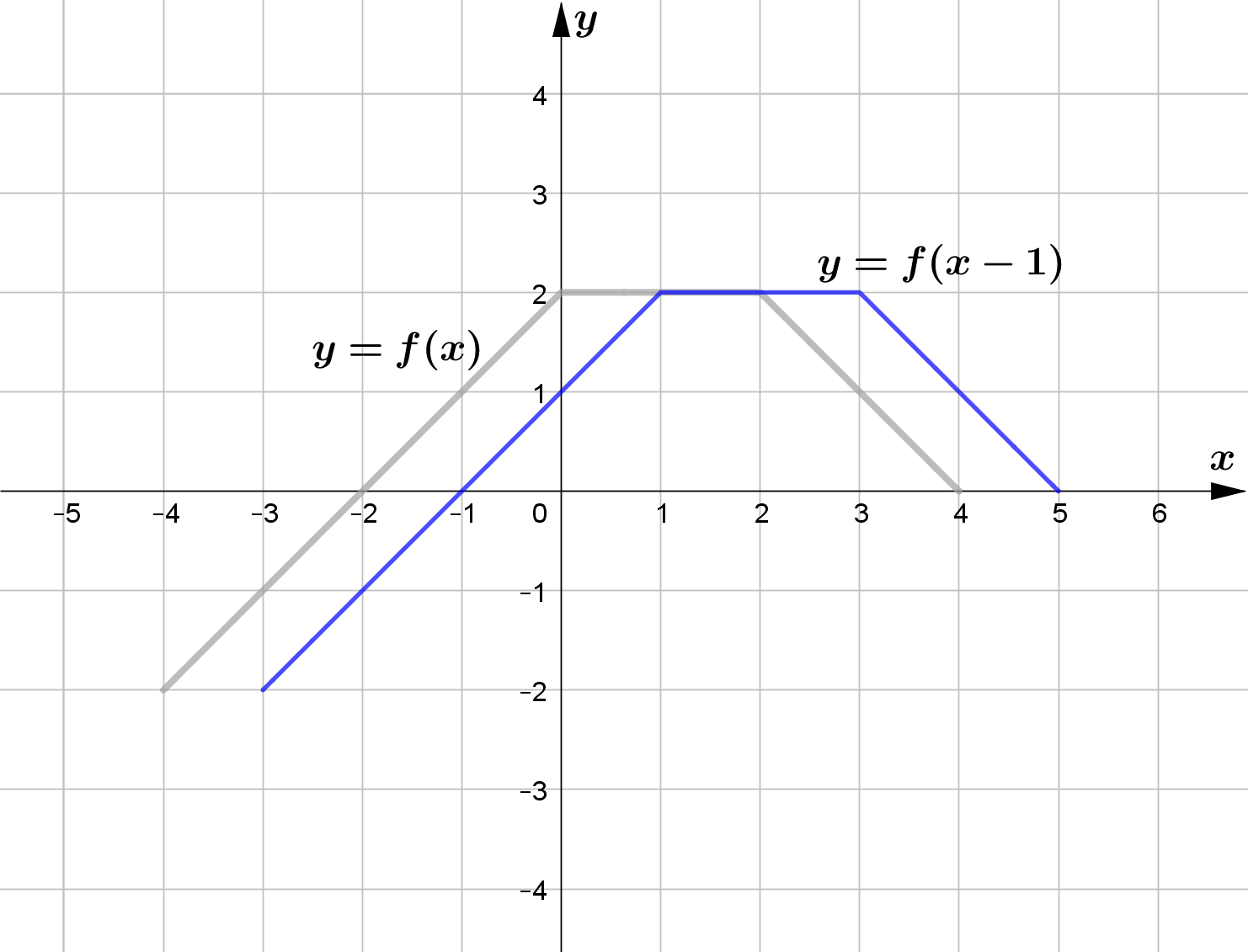
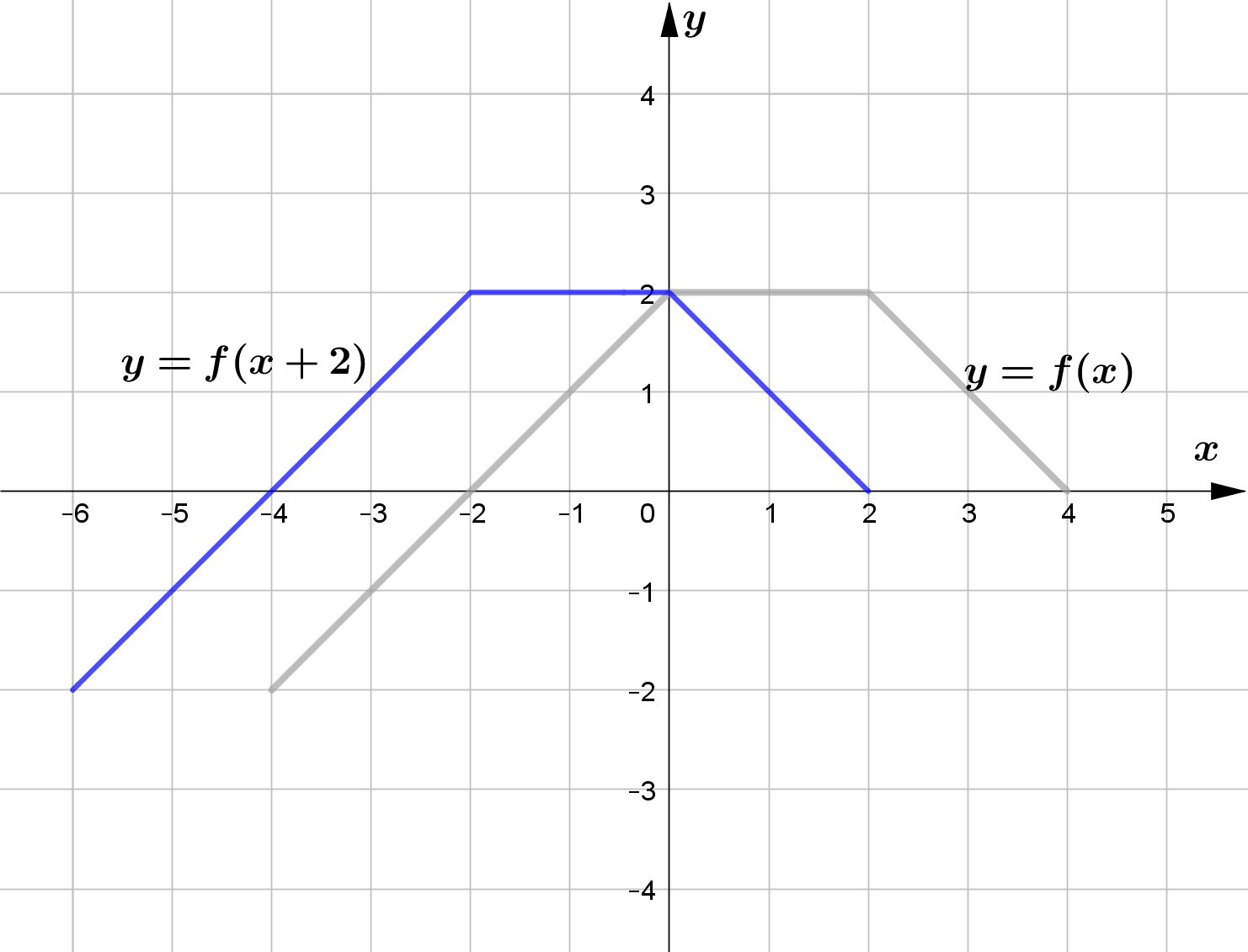
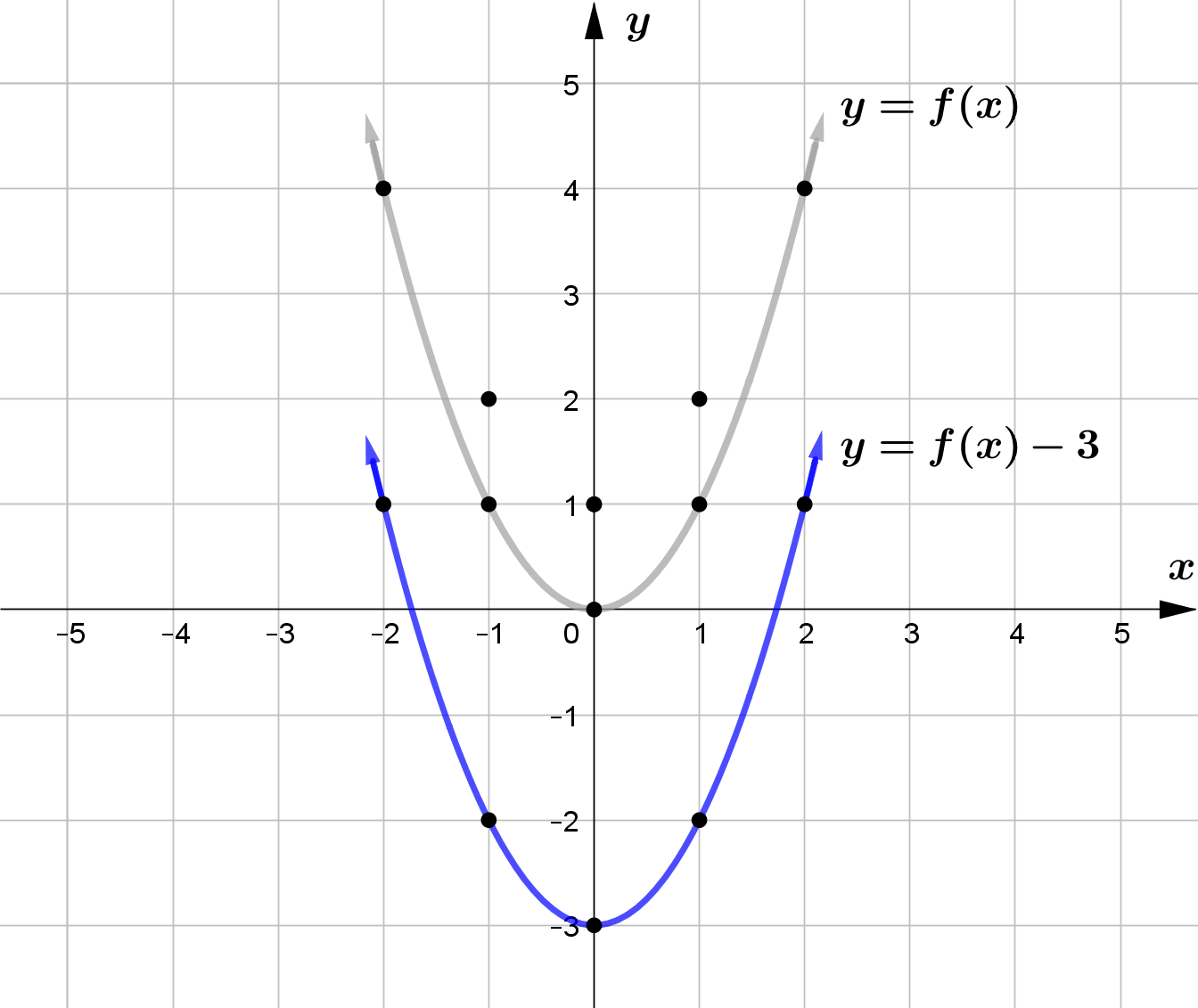
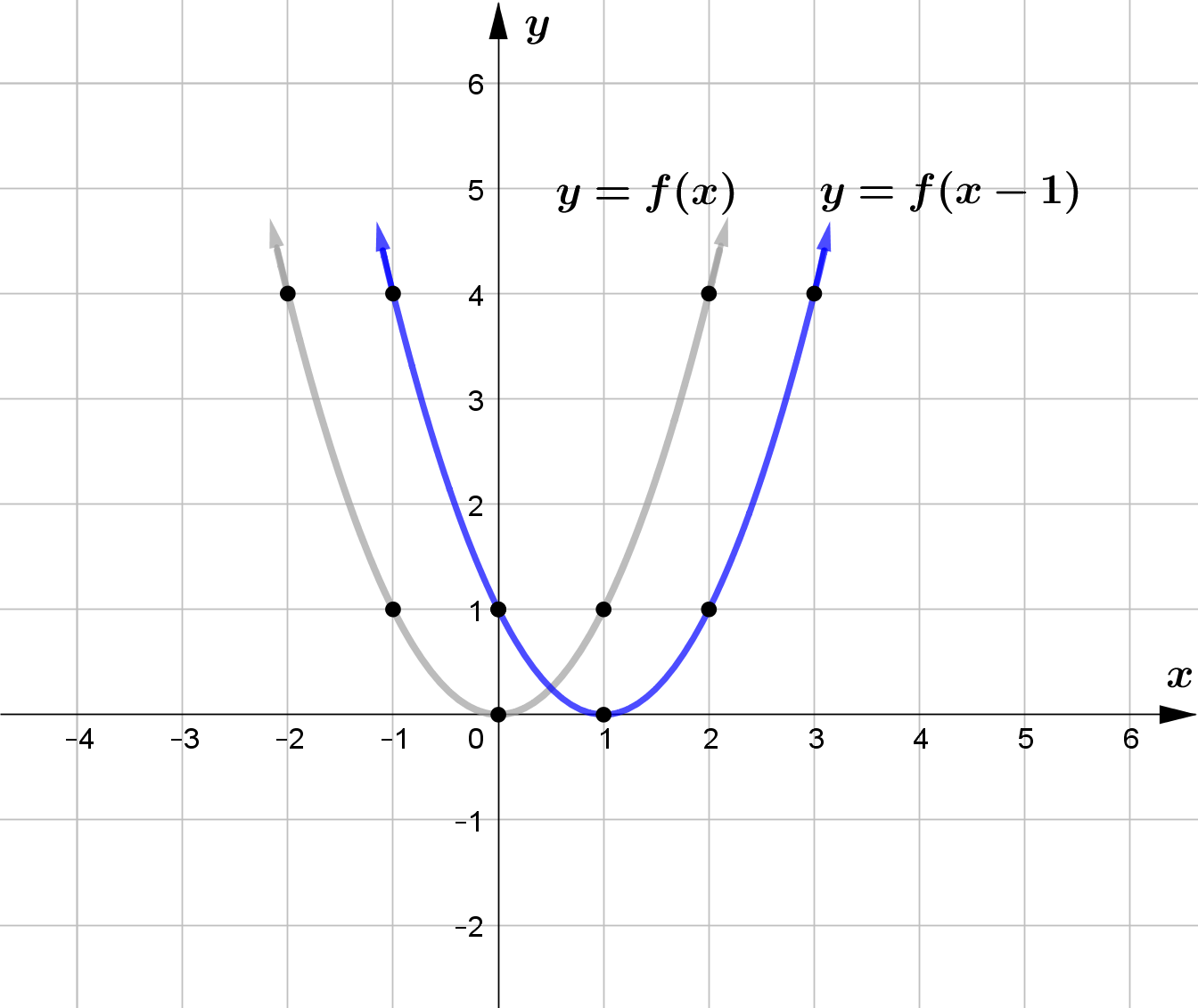
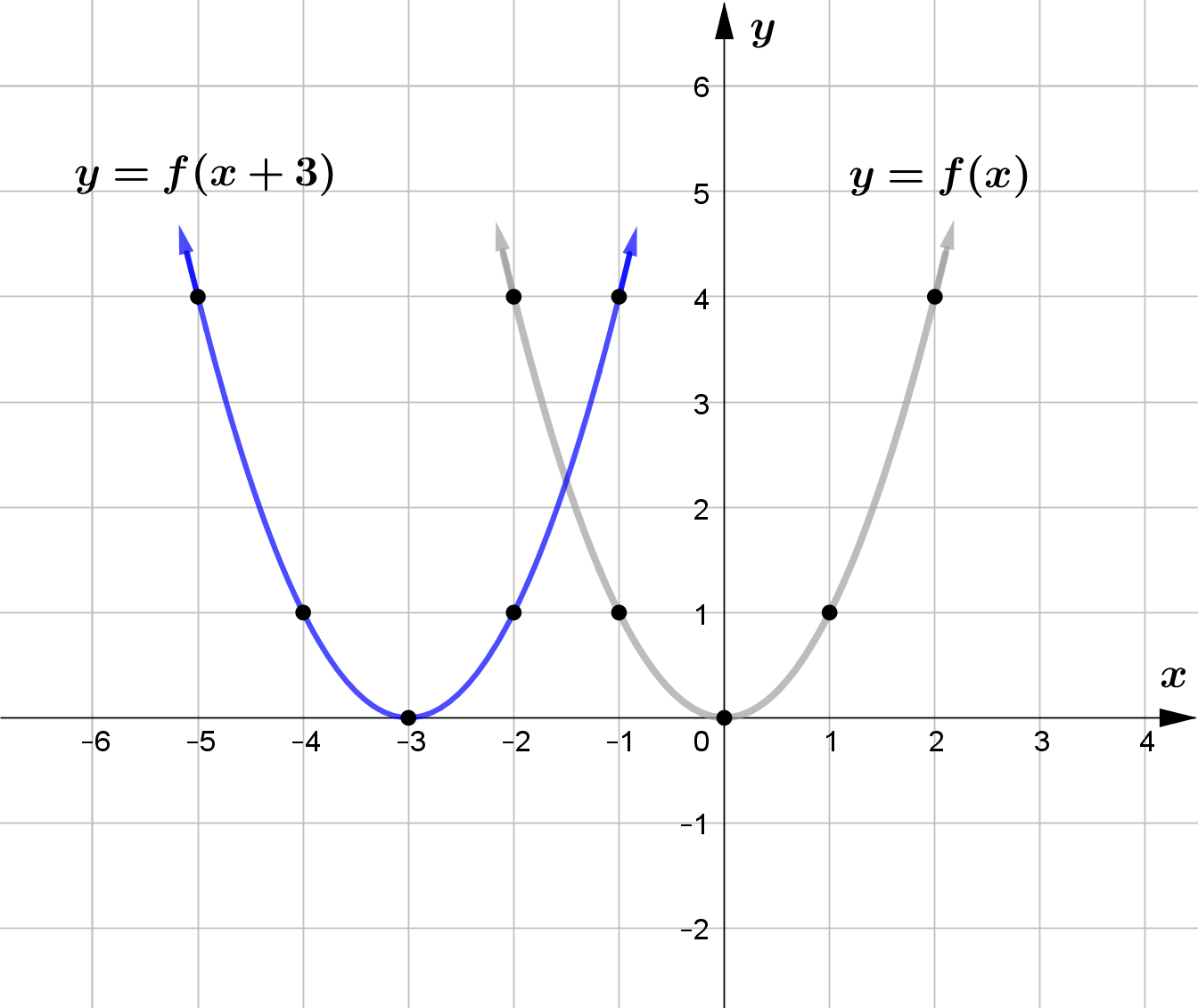
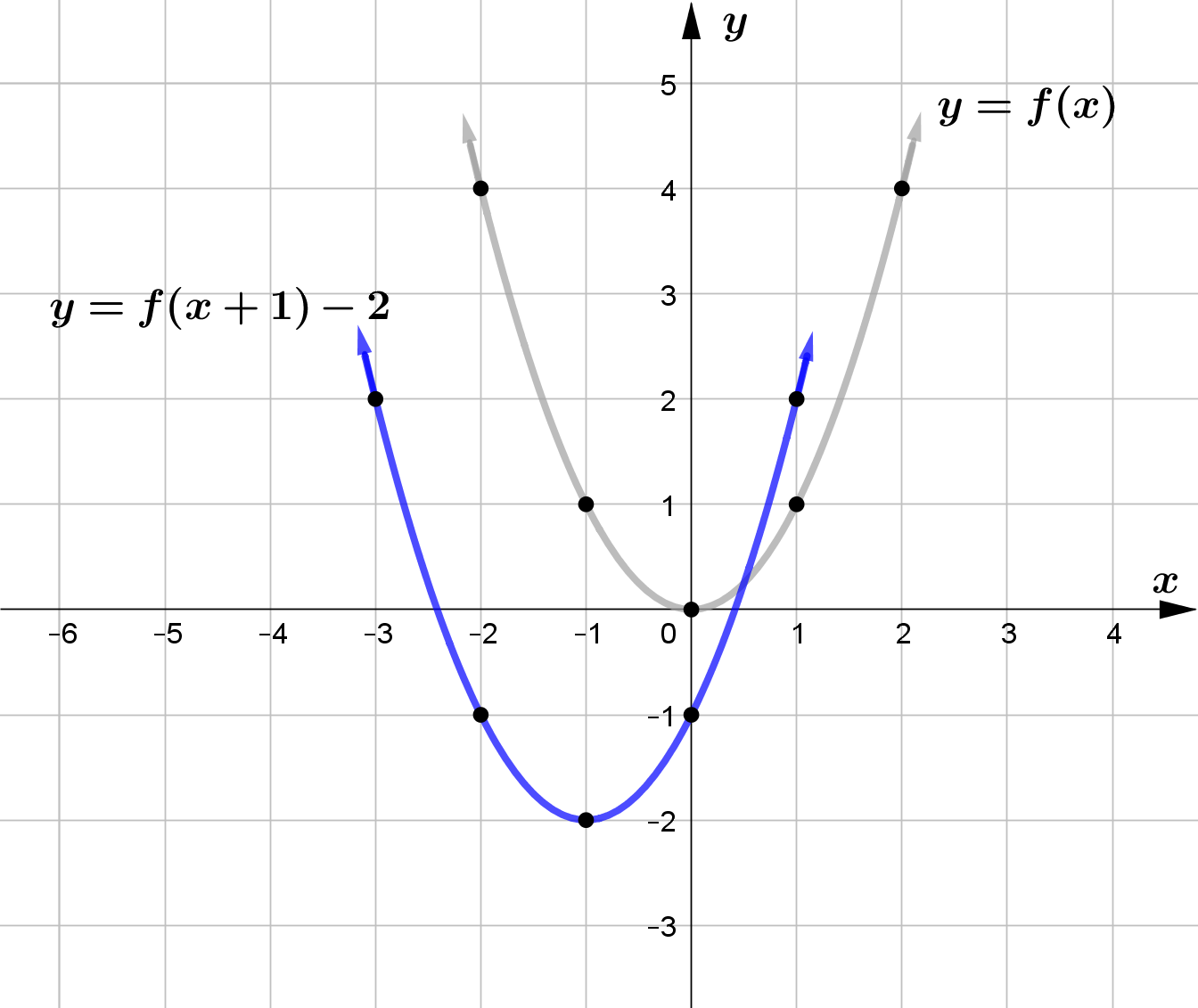
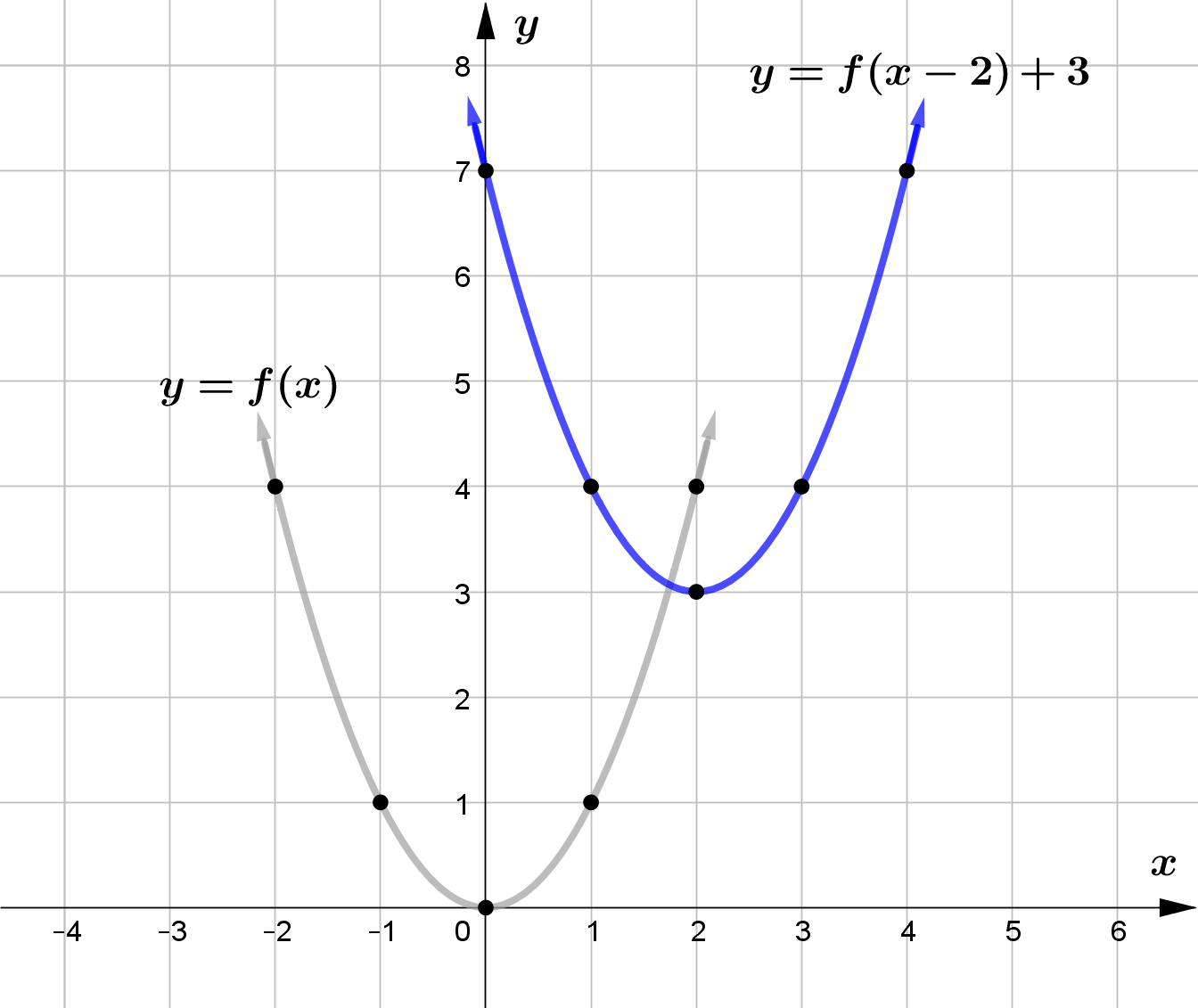
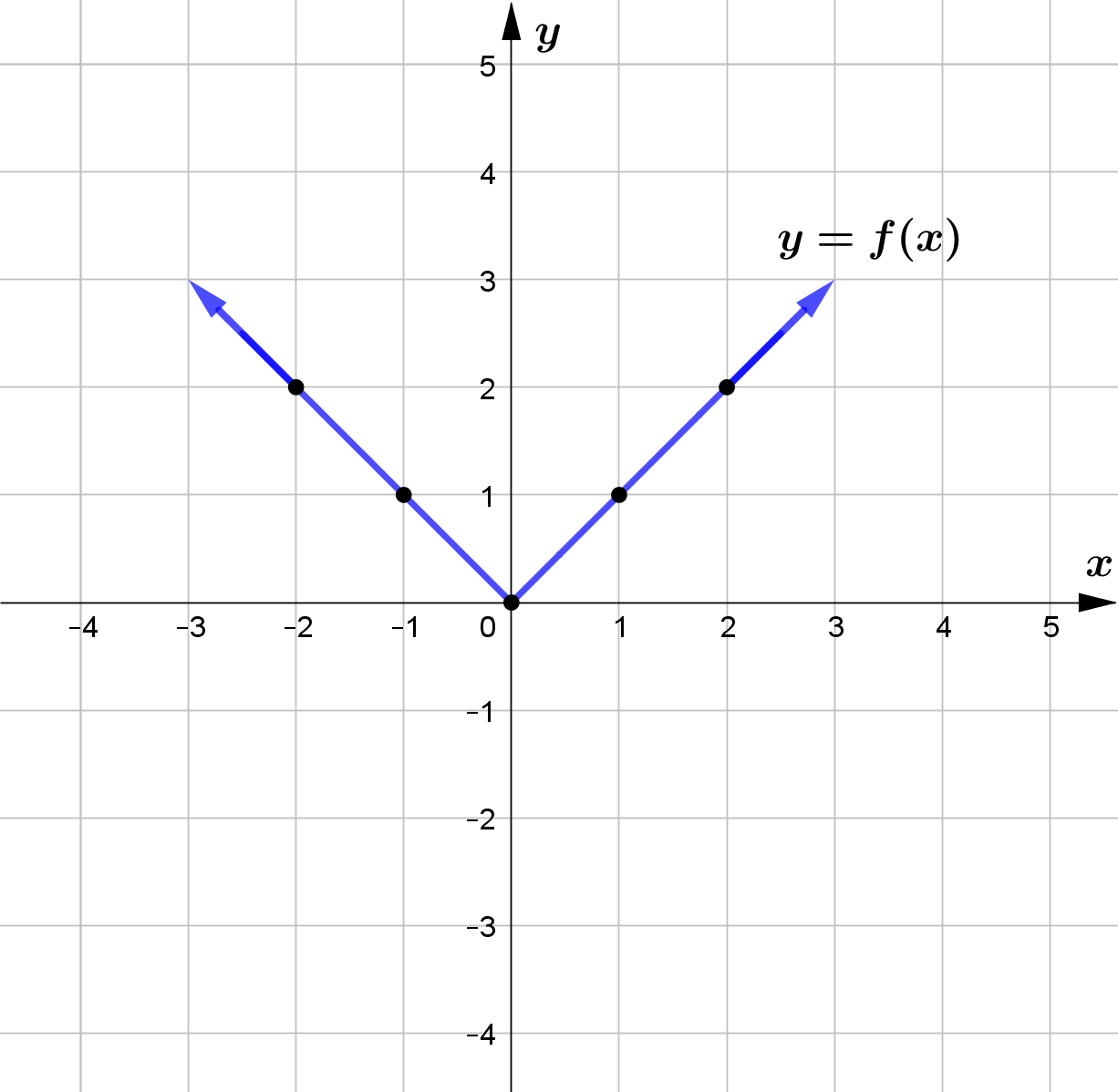
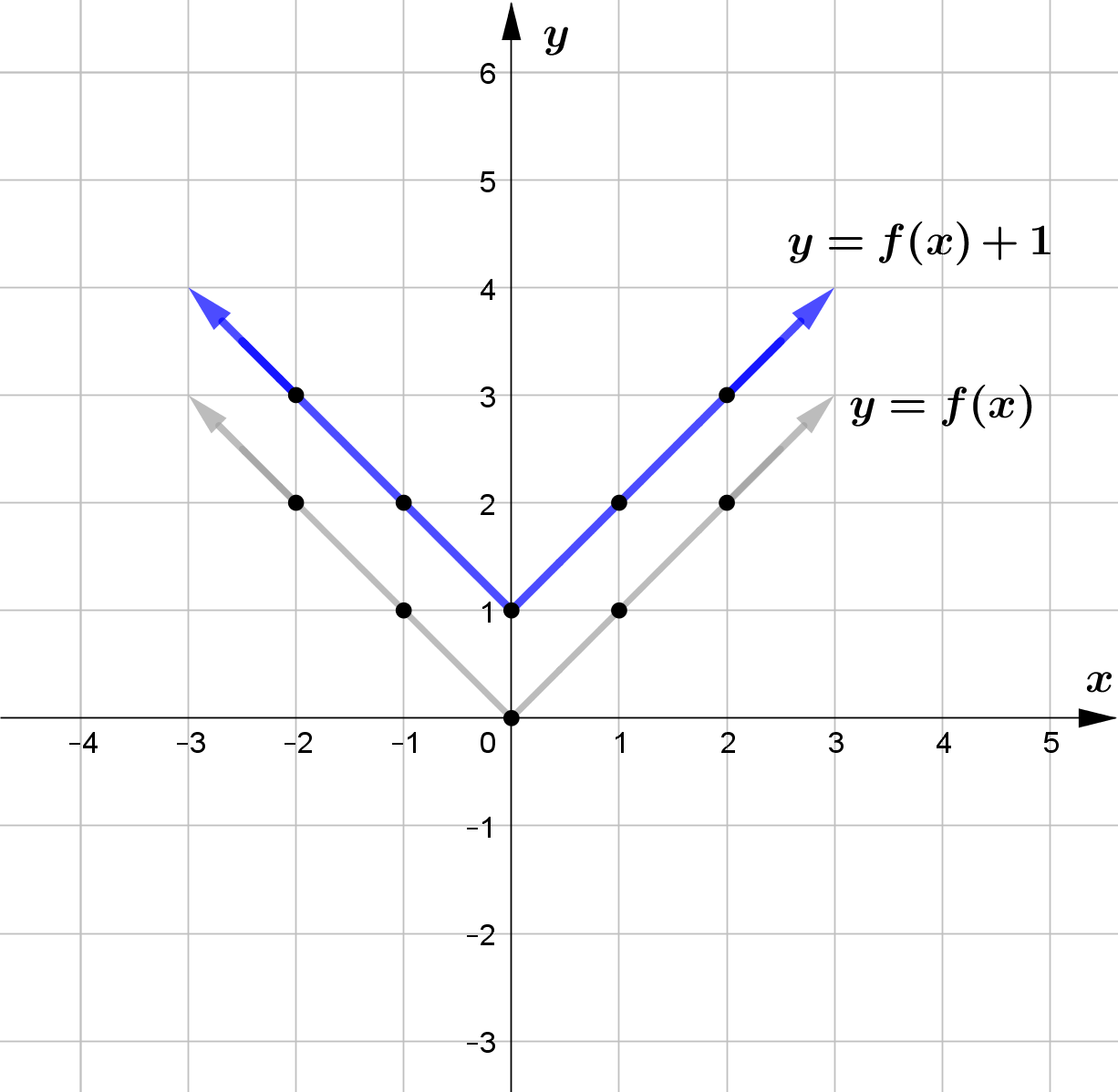
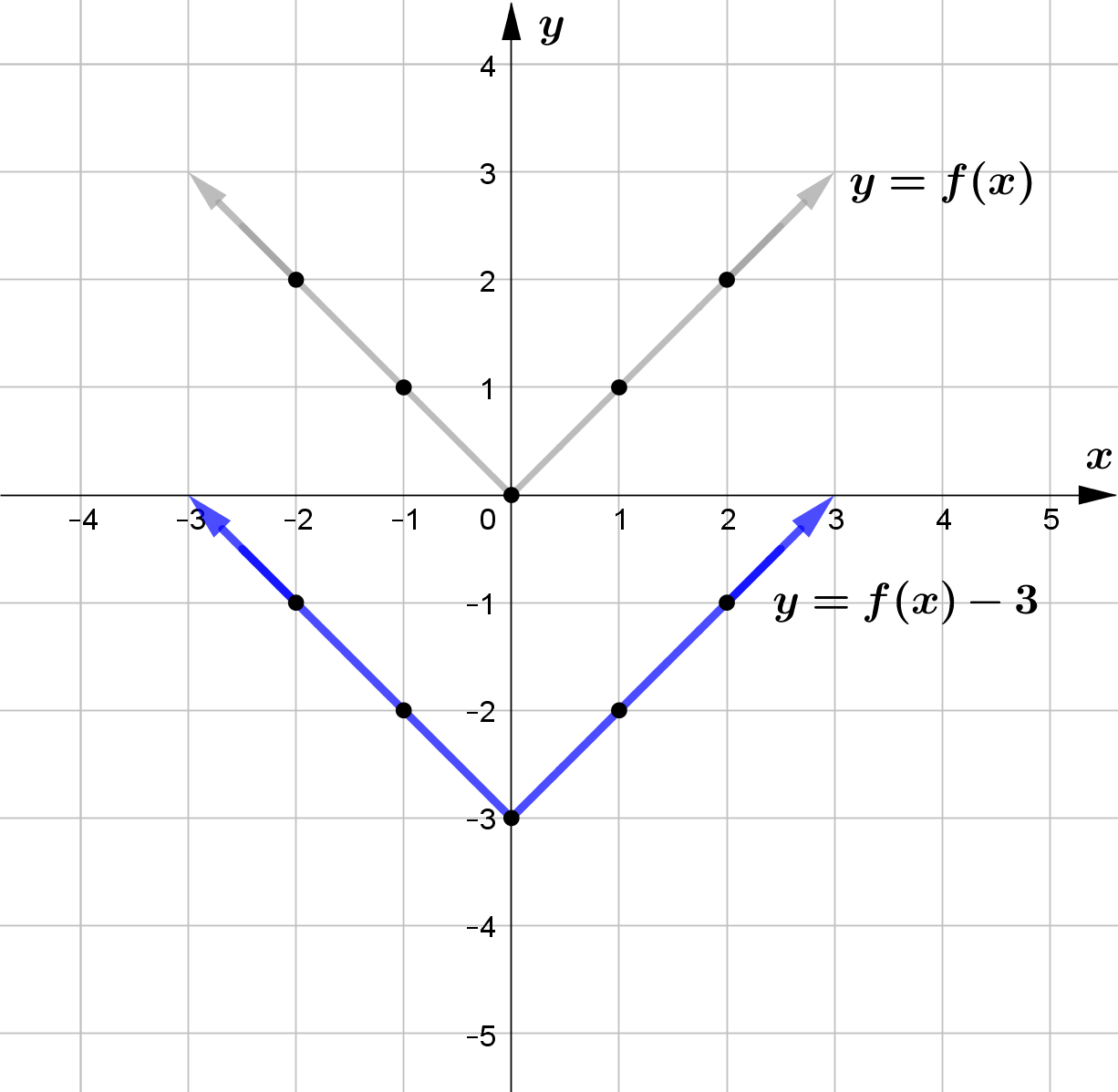
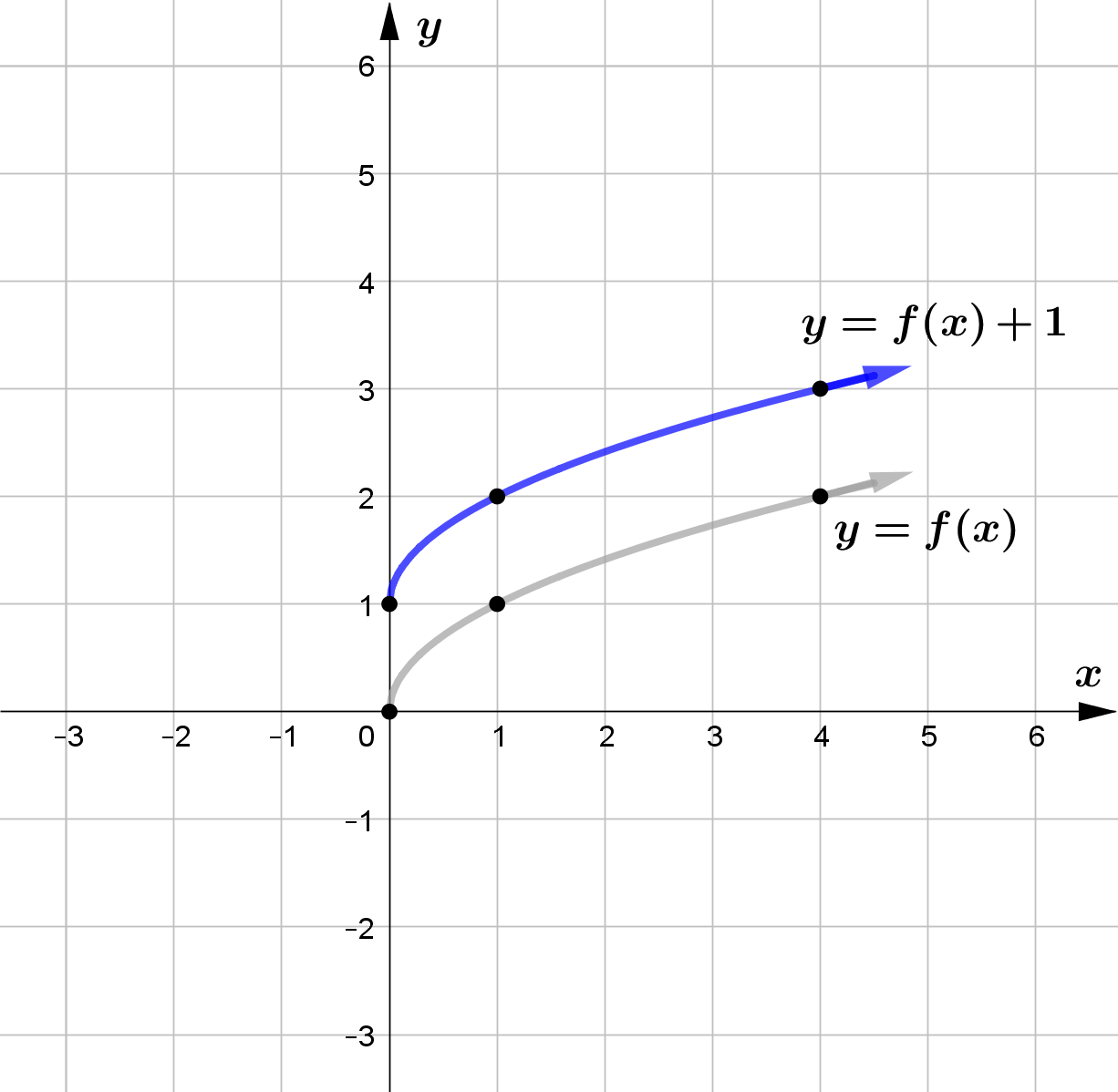
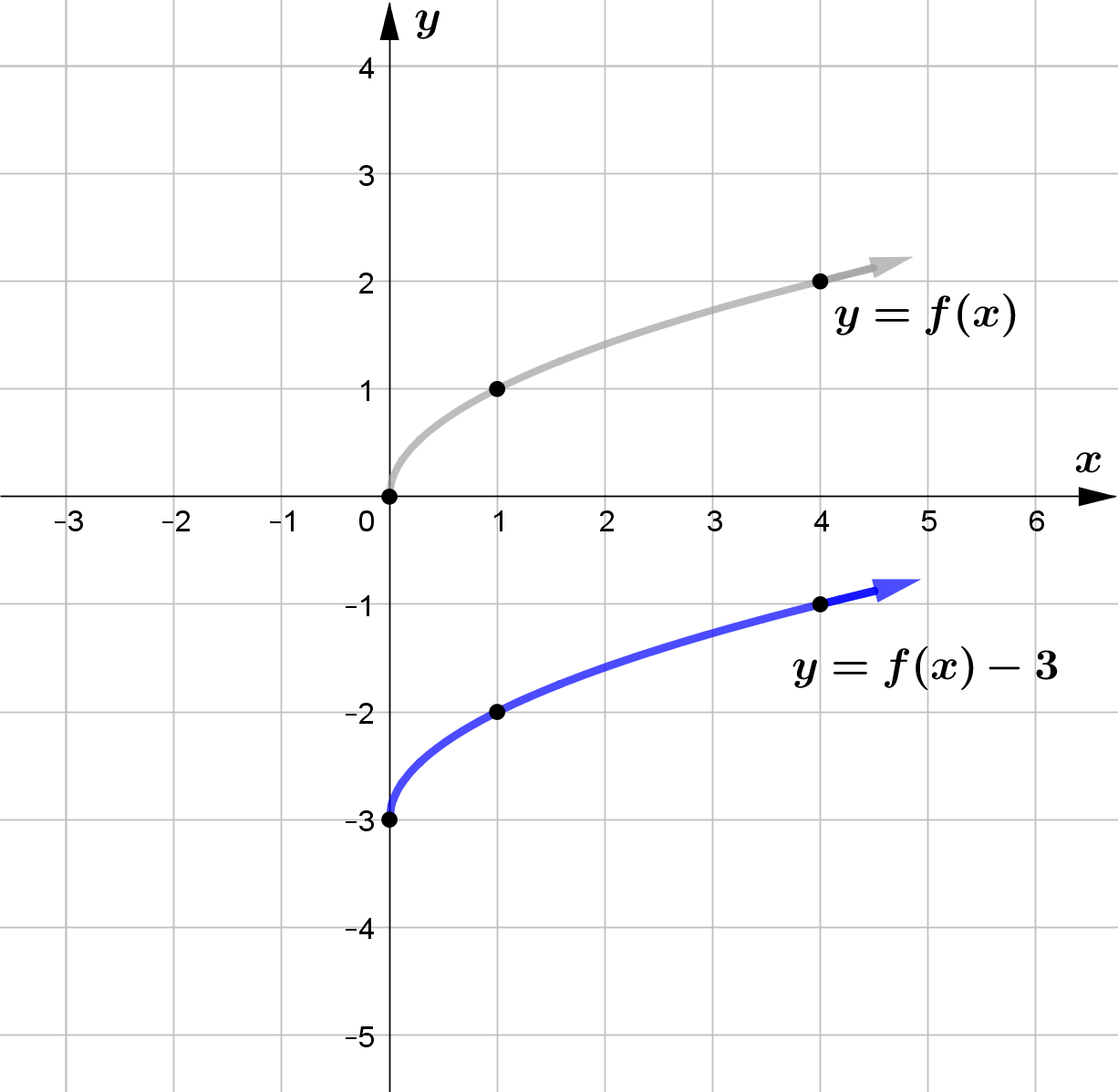
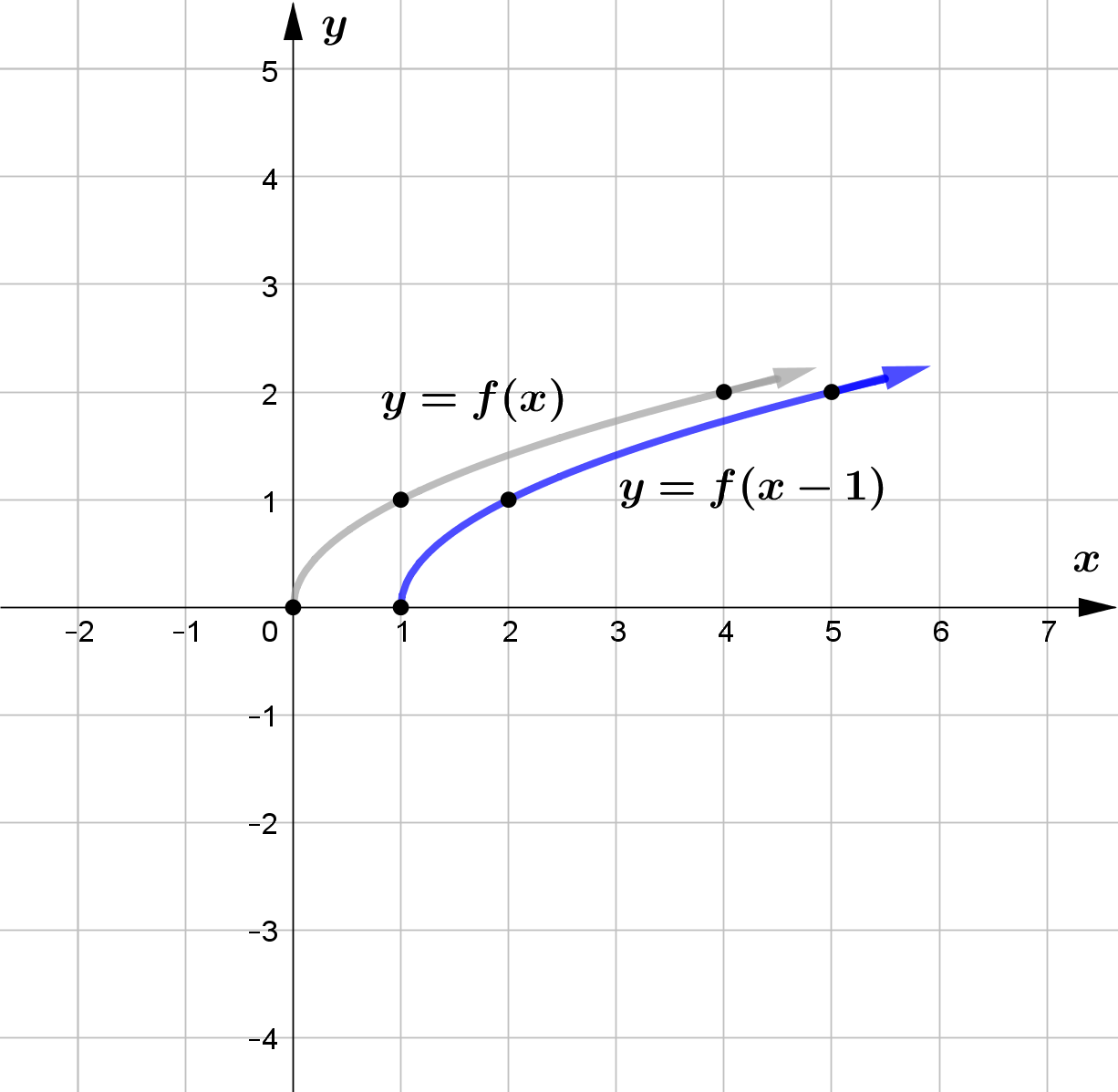
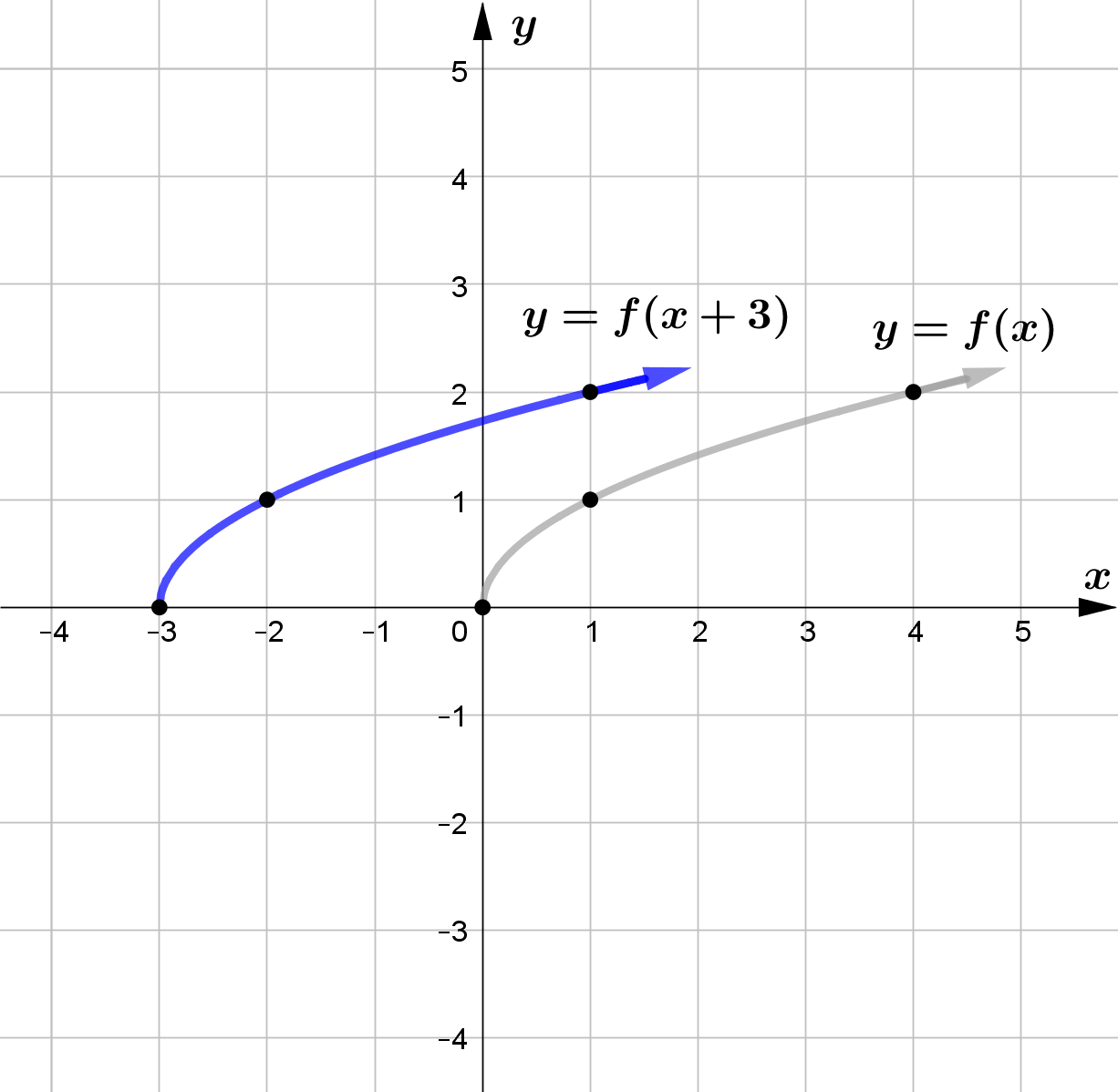
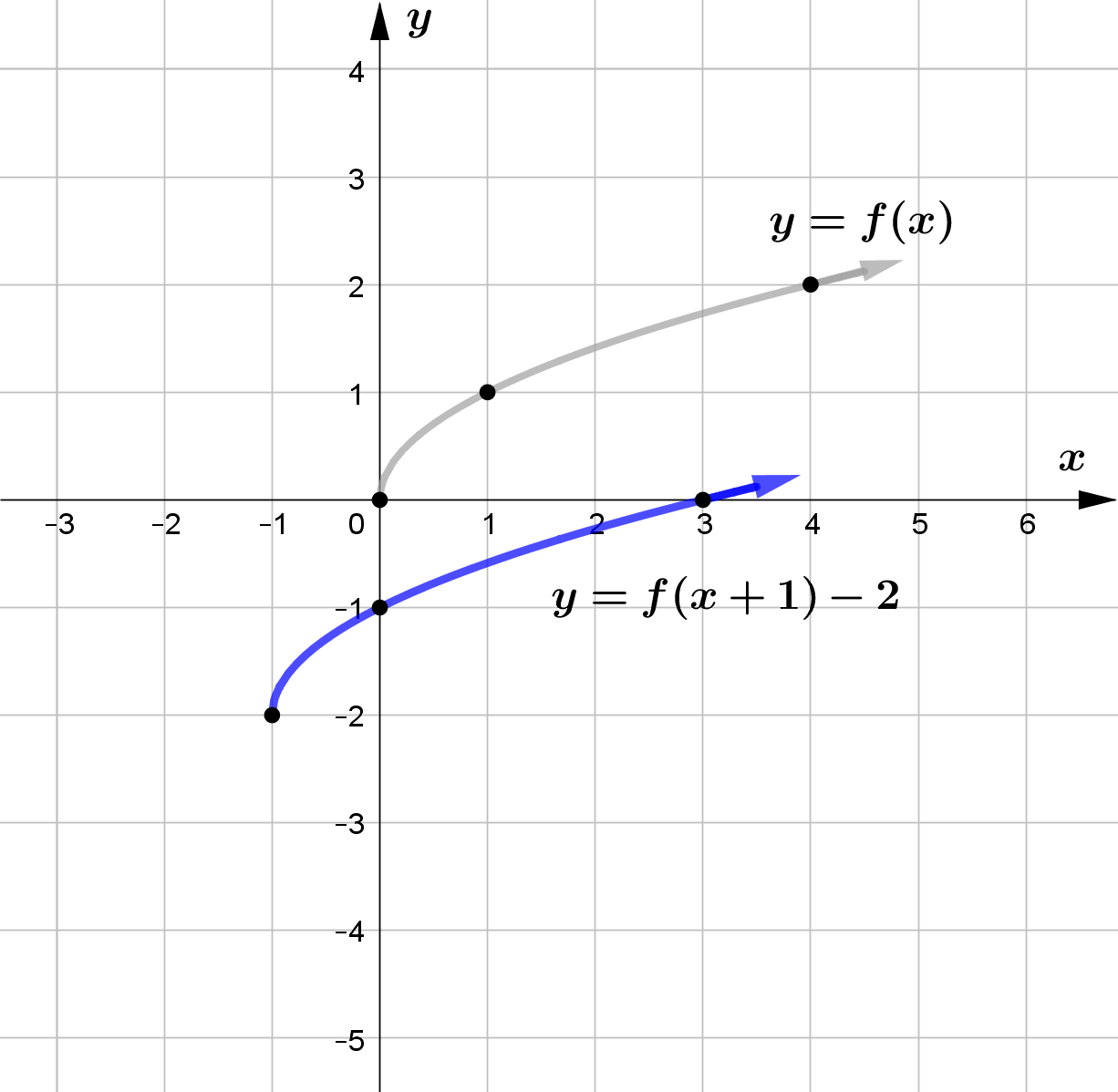
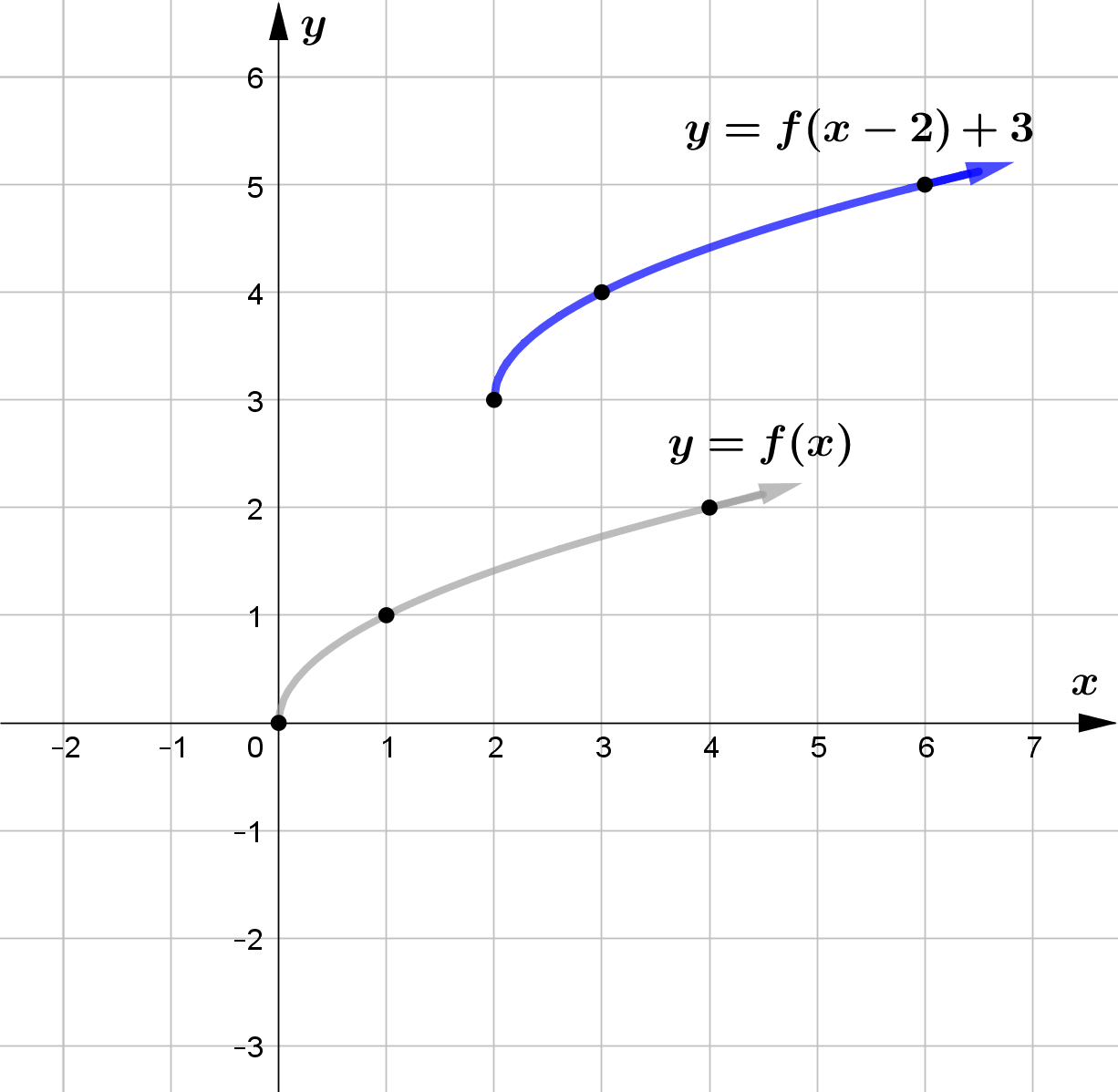
Vertical Translation
For any function $f(x)$ and $c>0$, $f(x)+c$ vertically shifts the graph of $f(x)$ upward by $c$ units
and $f(x)-c$ vertically shifts the graph of $f(x)$ downward by $c$ units.
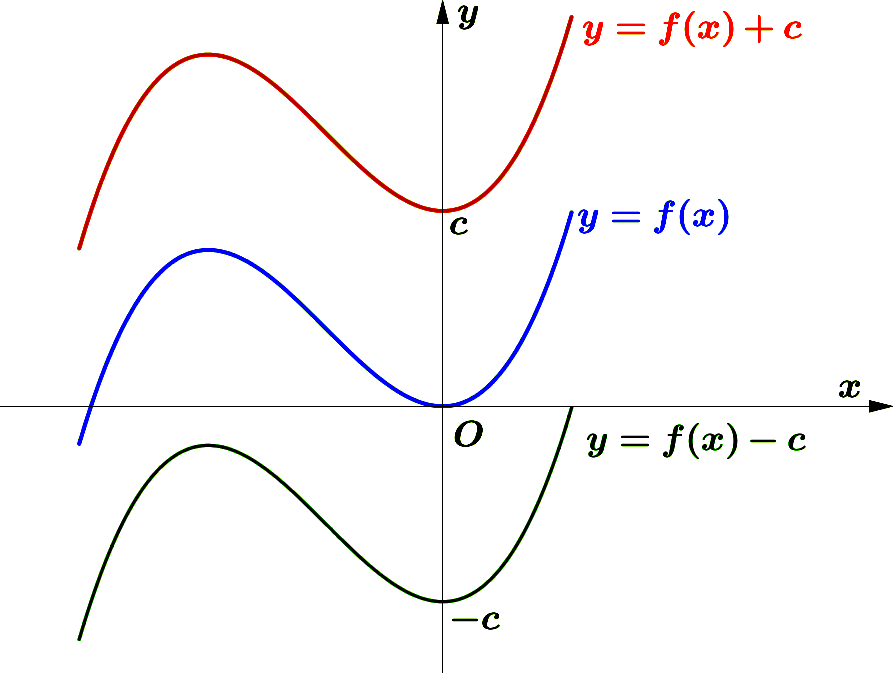
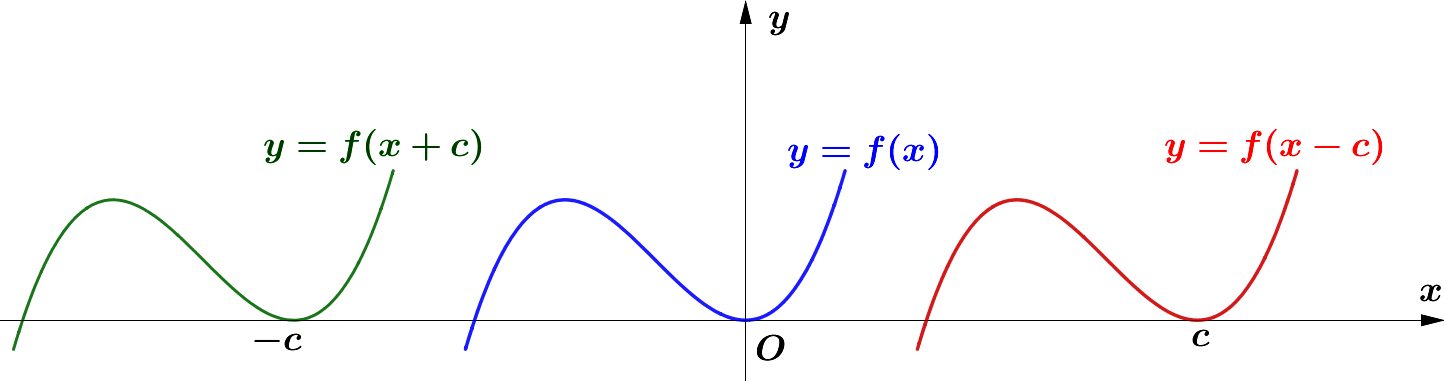
Horizontal Translation
For any function $f(x)$ and $c>0$, $f(x-c)$ horizontally shifts the graph of $f(x)$ right by $c$ units and
$f(x+c)$ horizontally shifts the graph of $f(x)$ left by $c$ units.
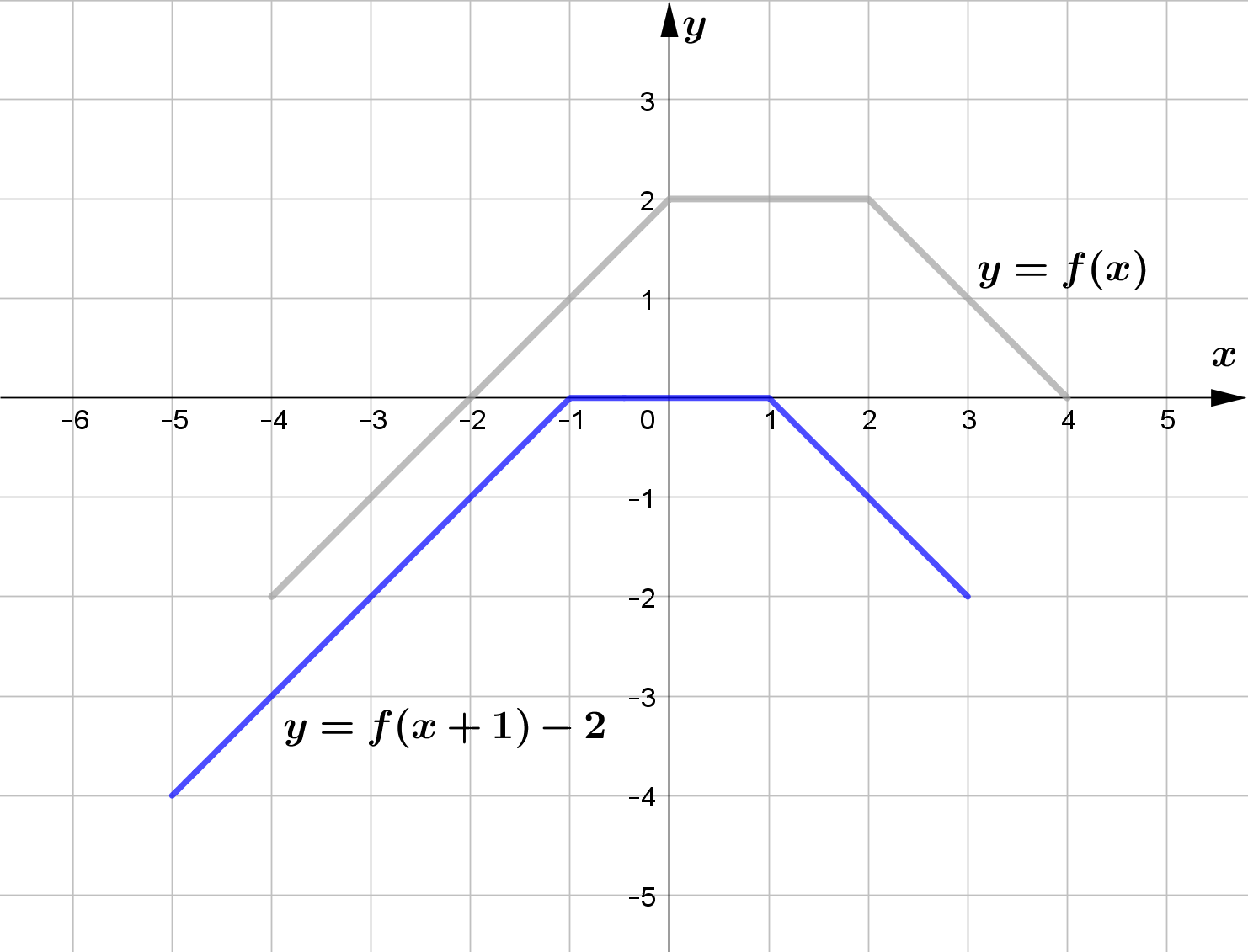
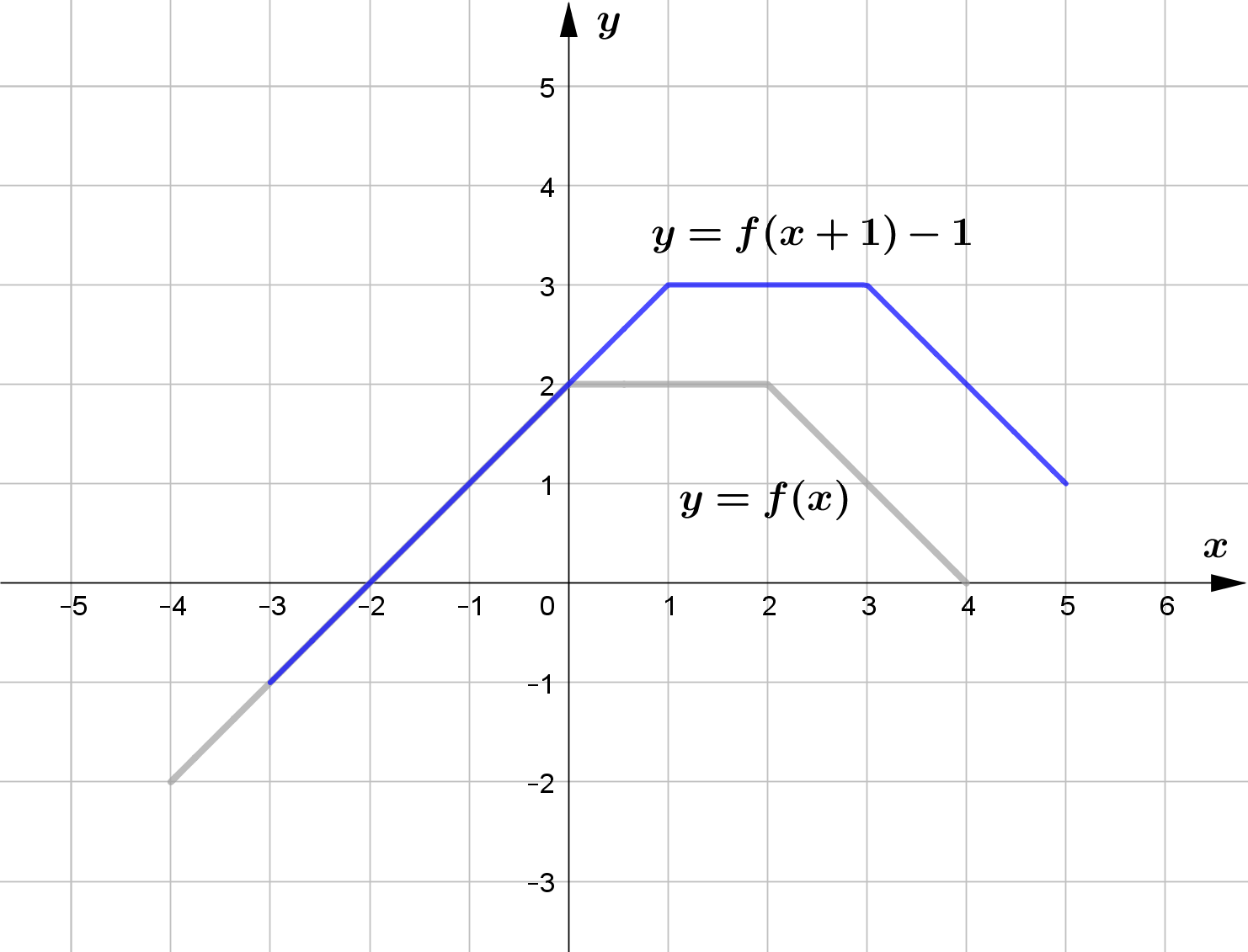
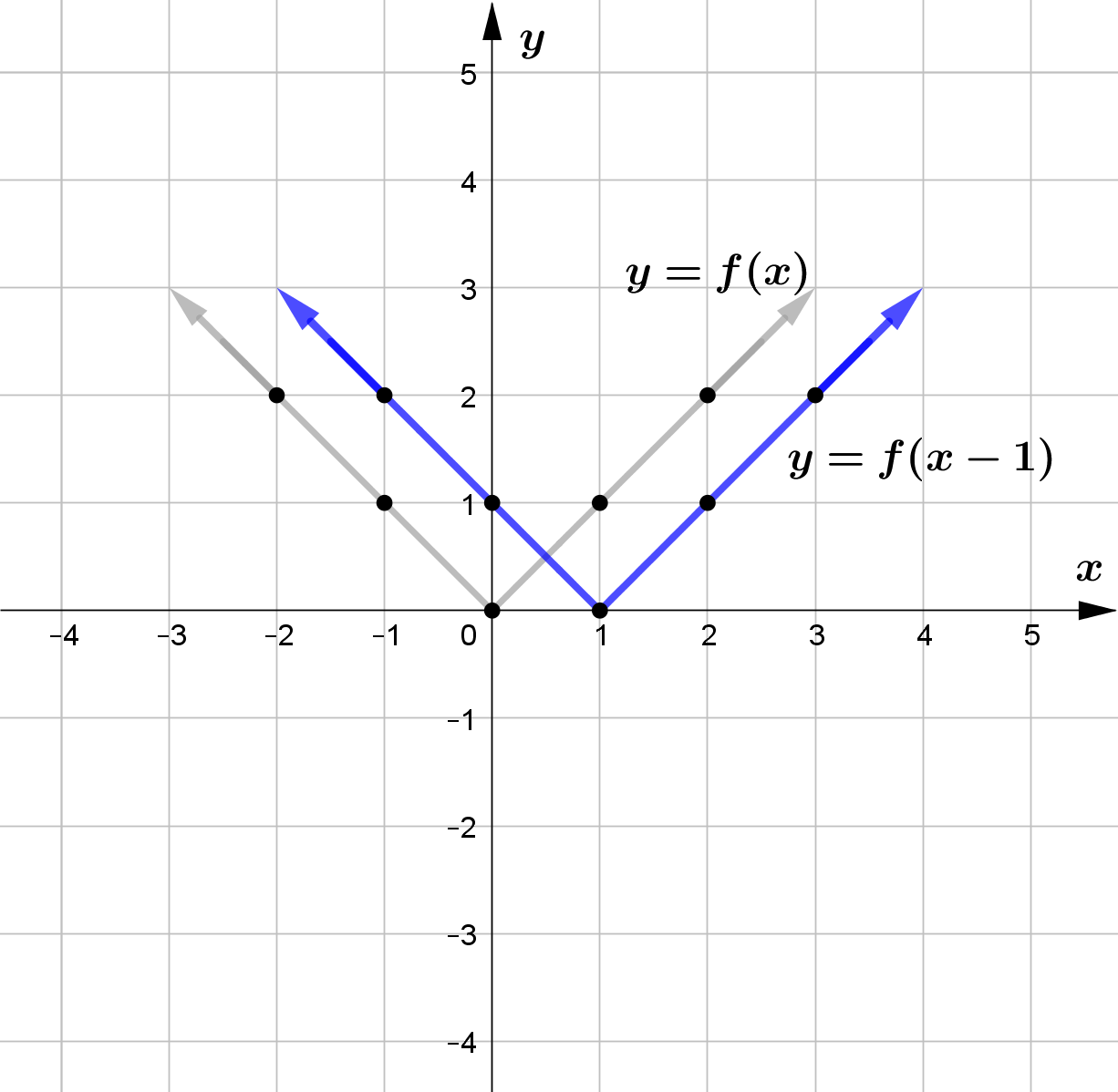
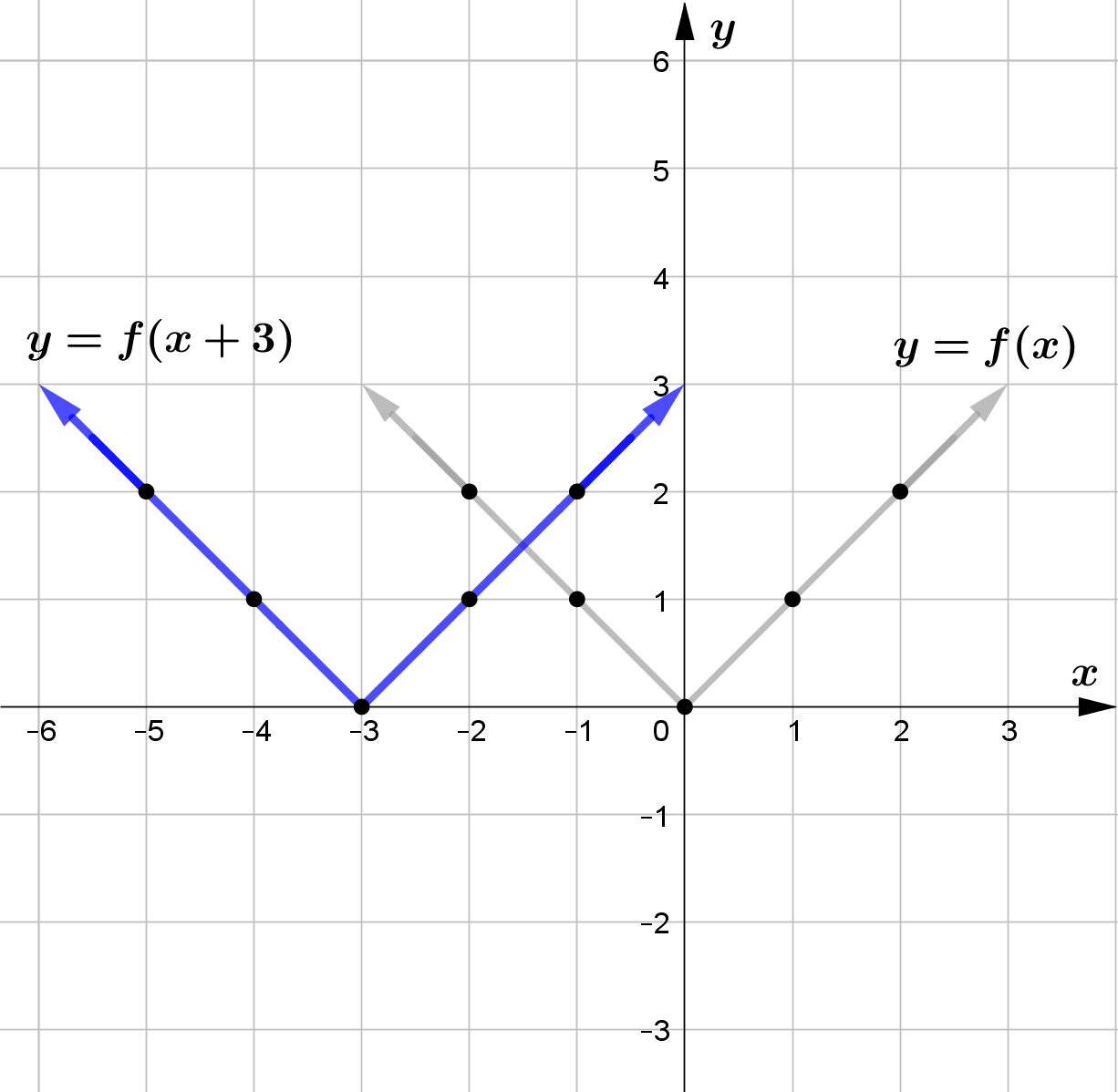
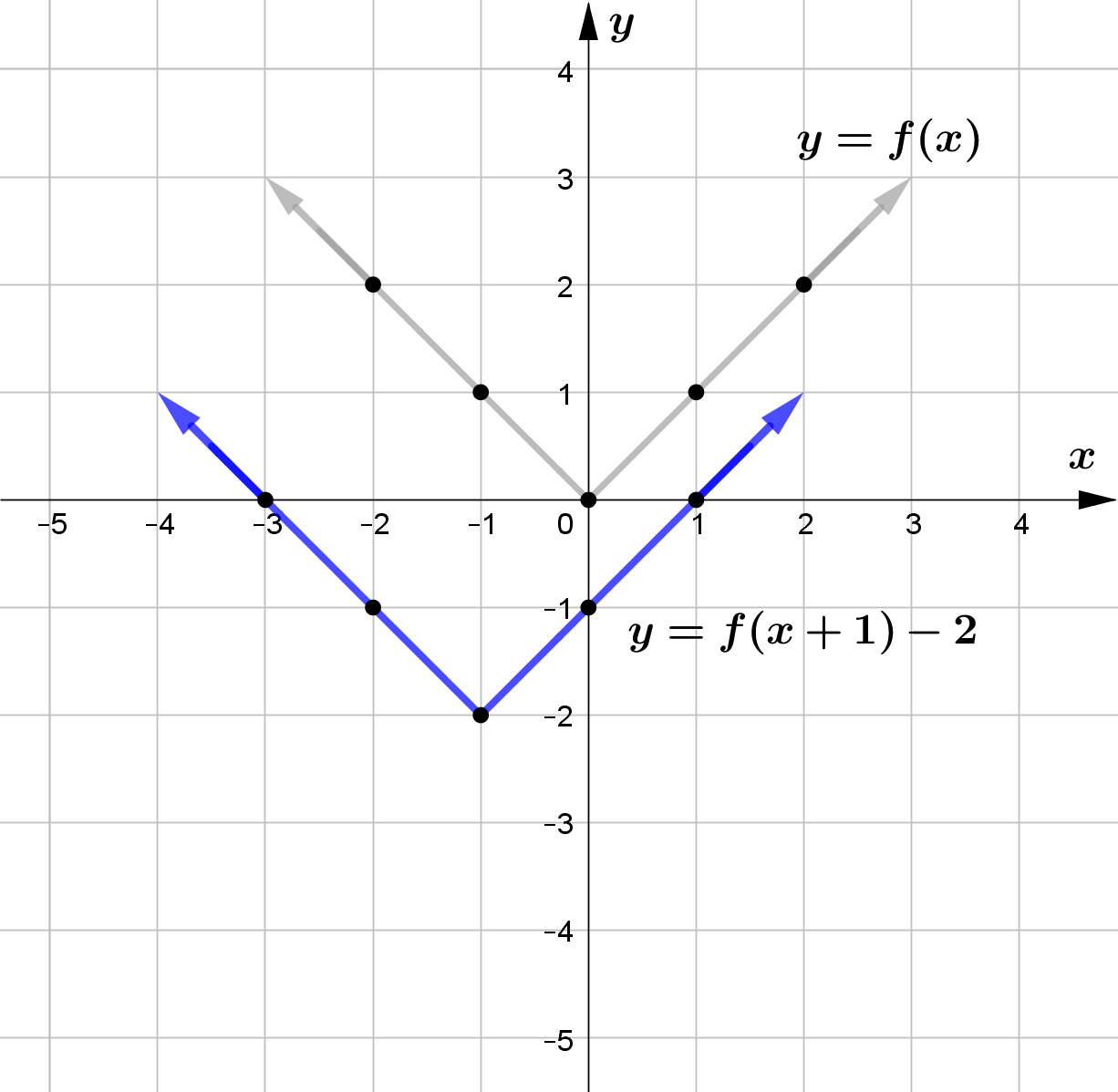
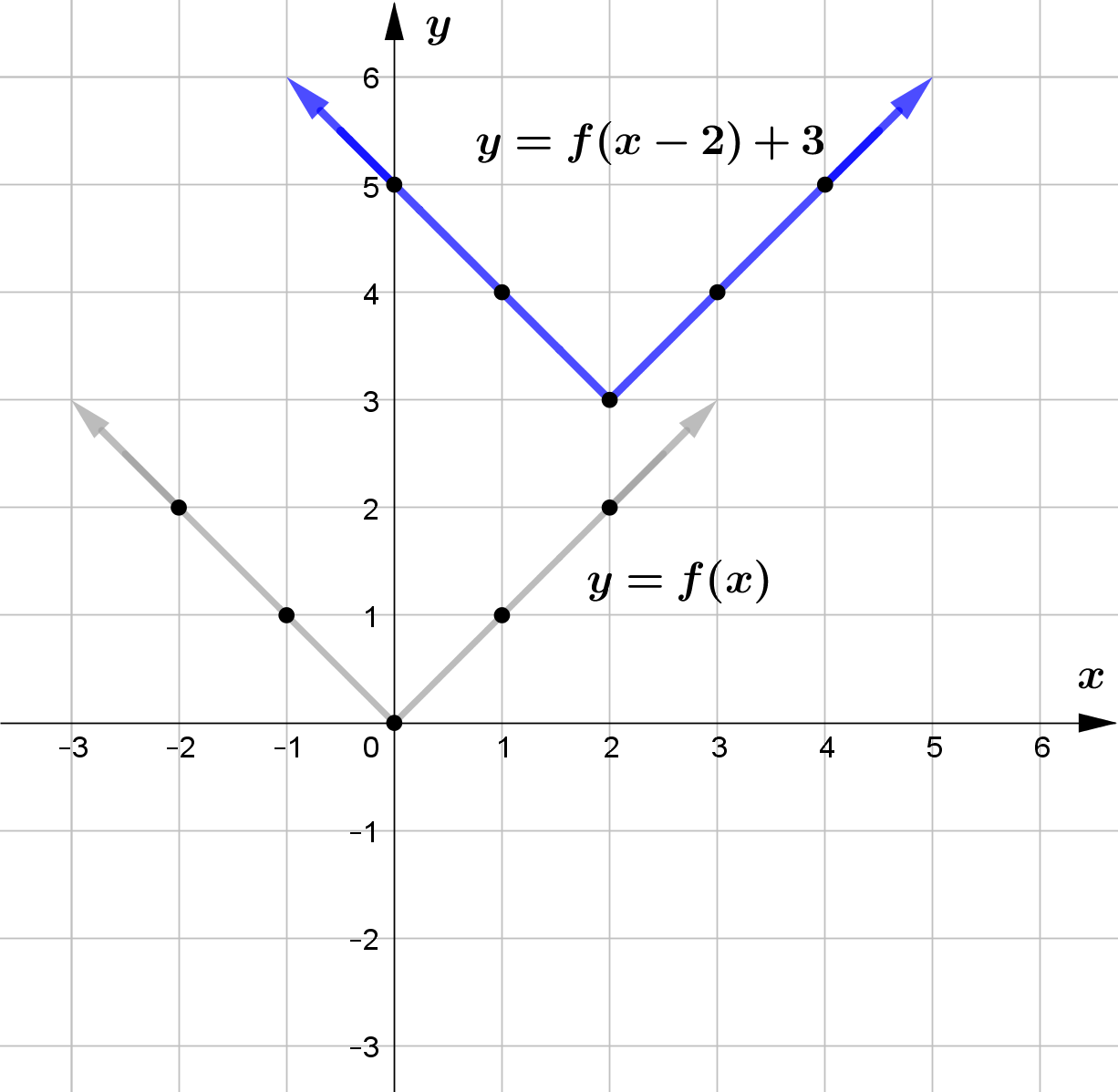
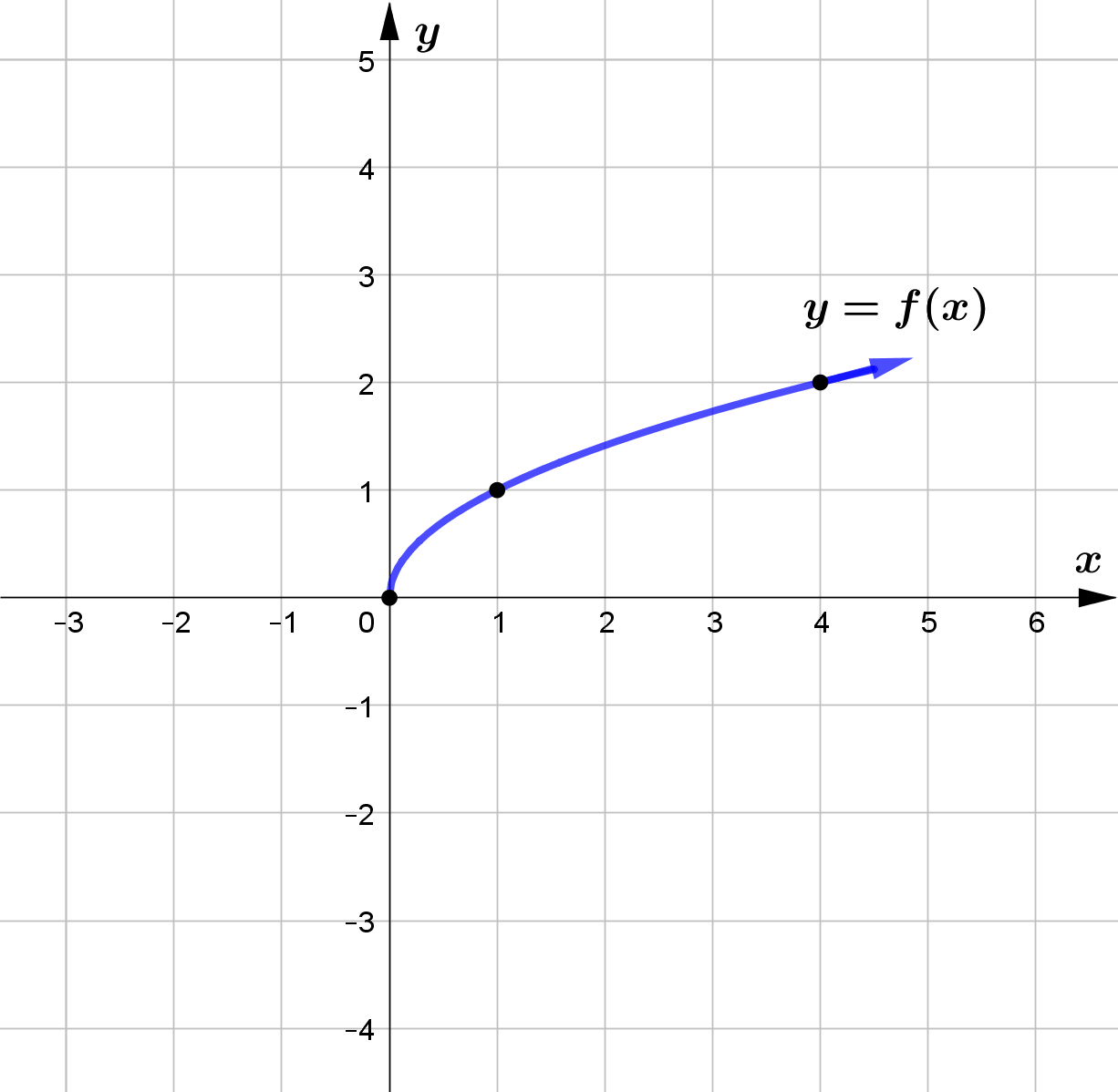
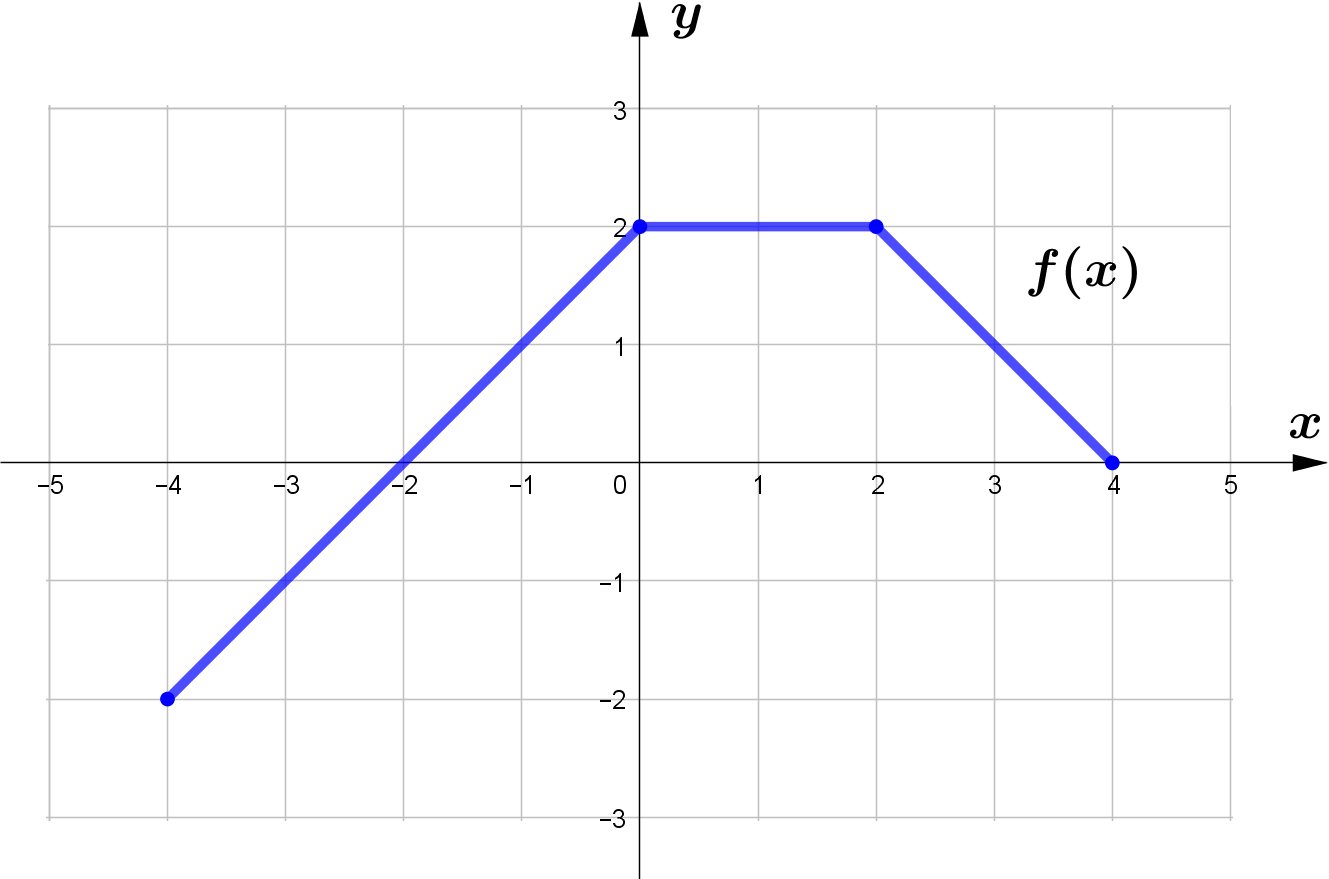
Question (1)
Use the graph of the function $f$ to sketch the graph of the following functions.
$\begin{array}{lll}
\text{(a) } g(x) = f(x) + 1 \\\\
\text{(b) } h(x) = f(x)-1 \\\\
\text{(c) } p(x) = f(x-1) \\\\
\text{(d) } F(x) = f(x+2) \\\\
\text{(e) } G(x) = f(x+1) - 2\\\\
\text{(f) } H(x) = f(x-1) + 1
\end{array}$
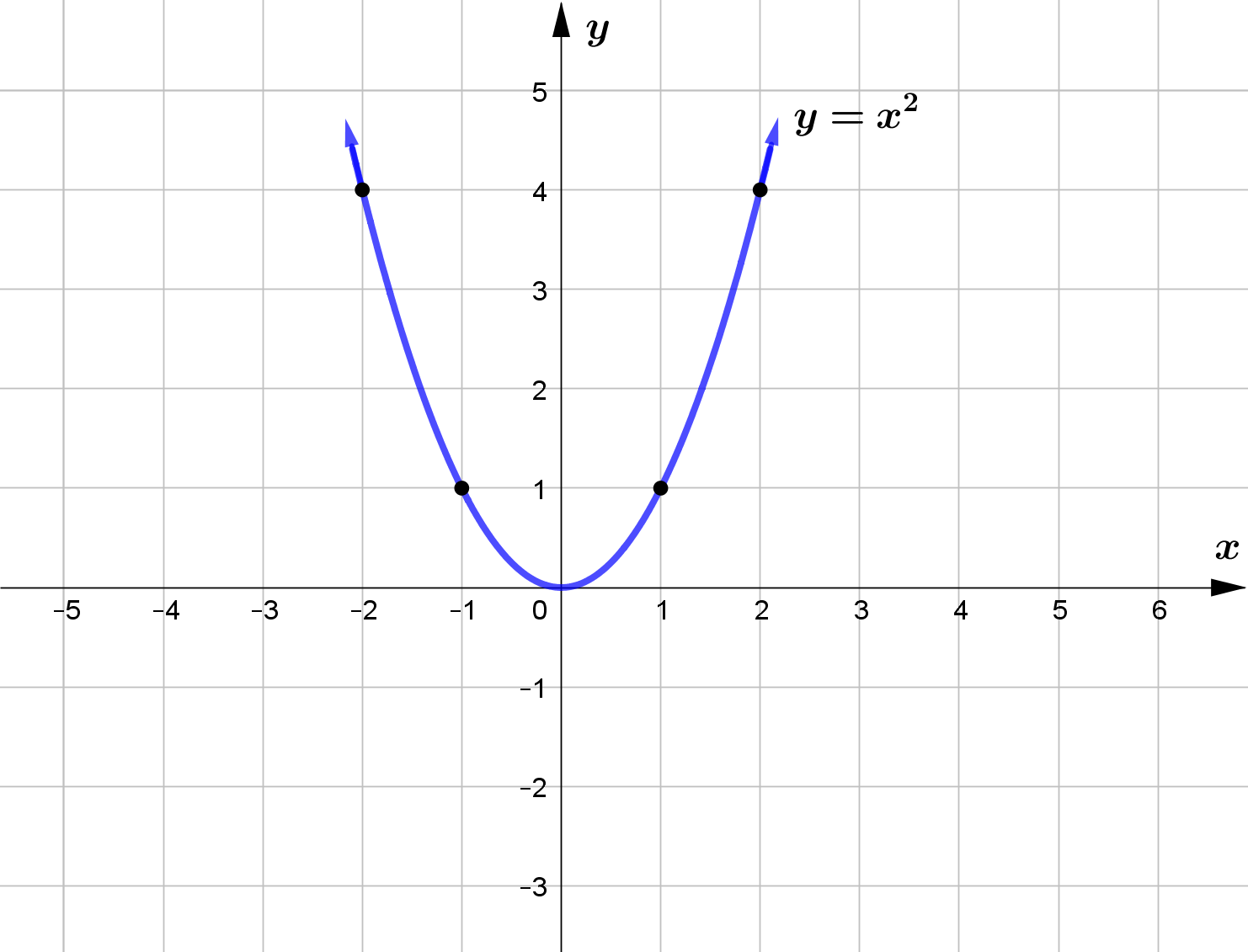
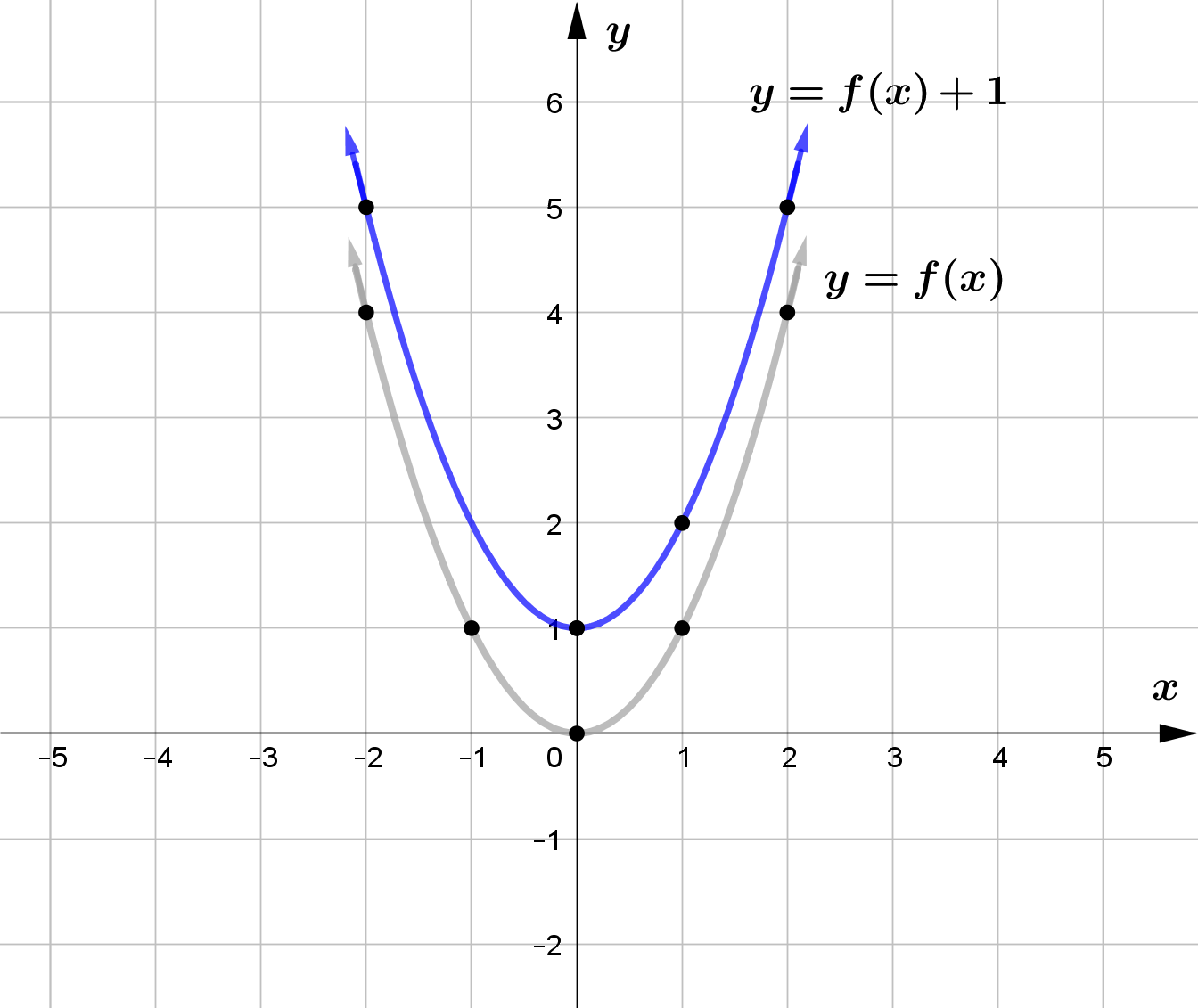
Question (2)
Draw the graph $f(x) = x^2$. Hence using the transformations of $f(x)$, draw the graph of the following functions.
$\begin{array}{lll}
\text{(a) } g(x) = f(x) + 1 \\\\
\text{(b) } h(x) = f(x) - 3 \\\\
\text{(c) } p(x) = f(x-1) \\\\
\text{(d) } F(x) = f(x+3) \\\\
\text{(e) } G(x) = f(x+1) - 2 \\\\
\text{(f ) } H(x) = f(x-2) + 3
\end{array}$
Question (3)
Draw the graph $f(x) = |x|$. Hence using the transformations of $f(x)$, draw the graph of the following functions.
$\begin{array}{lll}
\text{(a) } g(x) = f(x) + 1 \\\\
\text{(b) } h(x) = f(x) - 3 \\\\
\text{(c) } p(x) = f(x-1) \\\\
\text{(d) } F(x) = f(x+3) \\\\
\text{(e) } G(x) = f(x+1) - 2 \\\\
\text{(f ) } H(x) = f(x-2) + 3
\end{array}$
Question (4)
Draw the graph $f(x) = \sqrt{x}$. Hence using the transformations of $f(x)$, draw the graph of the following functions.
$\begin{array}{lll}
\text{(a) } g(x) = f(x) + 1 \\\\
\text{(b) } h(x) = f(x) - 3 \\\\
\text{(c) } p(x) = f(x-1) \\\\
\text{(d) } F(x) = f(x+3) \\\\
\text{(e) } G(x) = f(x+1) - 2 \\\\
\text{(f ) } H(x) = f(x-2) + 3
\end{array}$
Question (5)
If the graph of the quadratic function $f(x)$ has the vertex at $(-1,3)$, state the vertex after the given translations:
$\begin{array}{lll}
\text{(a) } f(x-2)+2\\\\
\text{(b) } f(x)-5 \\\\
\text{(c) } f(x+1)-3 \\\\
\text{(d) } f(x-6) \\\\
\text{(e) } f(x+1) - 2\qquad\quad \\\\
\text{(f) } f(x+2) + 1
\end{array}$
Question (6)
If the points $A(2,-3)$ lies on the graph of $y=f(x)$. Use transformation to find the map point of $A$
on the graph $y= g(x)$ such that
(a) $g(x) = f(x-2) + 1$.
(b) $g(x) = f(x+1) - \frac{1}{2}$.
Question (7)
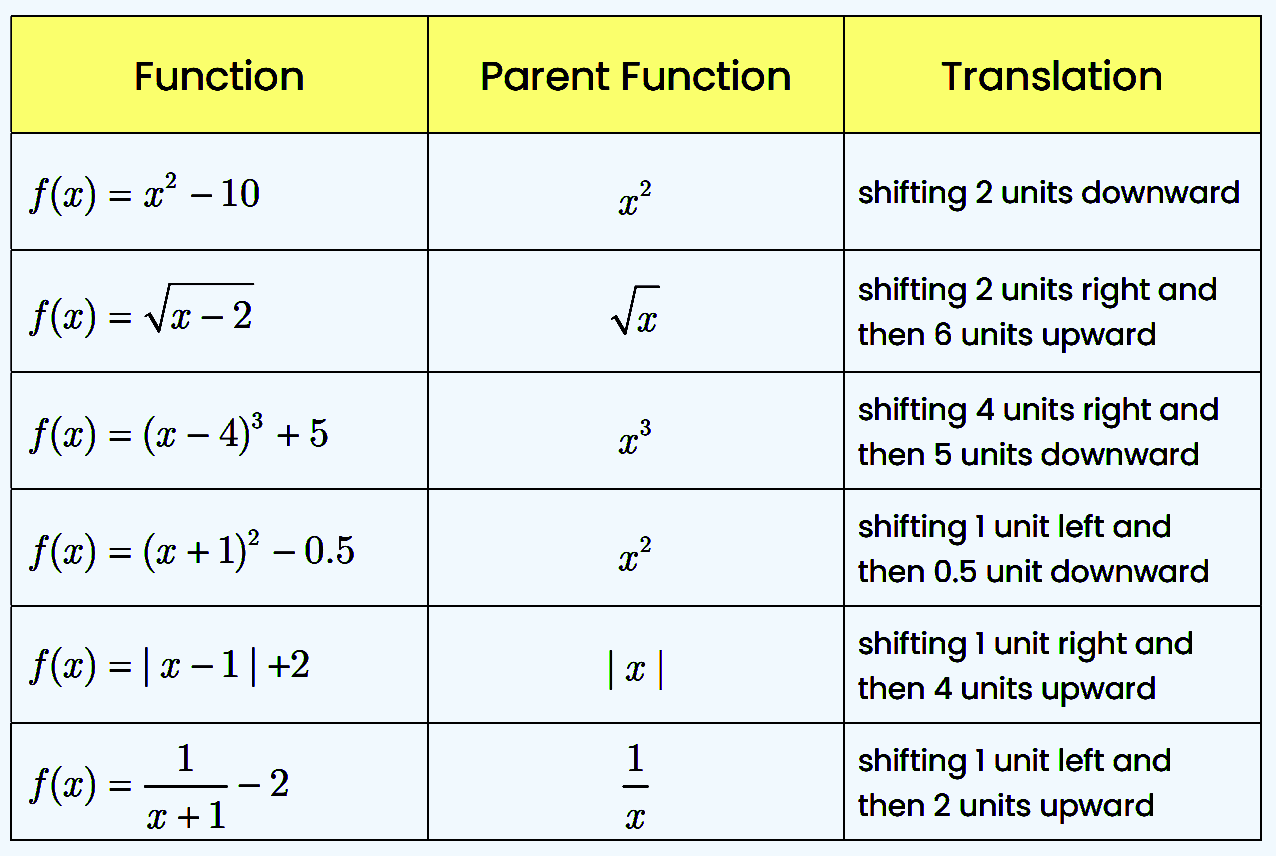
State the parent function and the translation that is occurring in each of the following functions.