May-Jun-21-p1-CIE-0606/12 : Solution

2021 (May-June) CIE (0606-Additional Mathematics), Paper 1/12 ၏ Question နှင့် Solution များ ဖြစ်ပါသည်။ Question Paper ကို ဒီနေရာမှာ Download ယူနိုင်ပါသည်။

1. Write $\dfrac{(p q r)^{-2} r^{\frac{1}{3}}}{\left(p^{2} r\right)^{-1} q^{3}}$ in the form $p^{a} q^{b} r^{c}$, where $a, b$ and $c$ are constants. [3]
   






$\begin{aligned} & \dfrac{(p q r)^{-2} r^{\frac{1}{3}}}{\left(p^{2} r\right)^{-1} q^{3}} \\\\ =& \dfrac{p^{-2} q^{-2} r^{-2} r^{\frac{1}{3}}}{p^{-2} r^{-1} q^{3}} \\\\ =& p^{-2+2} q^{-2-3} r^{\frac{1}{3}+1} \\\\ =& p^{0} q^{-5} r^{\frac{4}{3}} \end{aligned}$




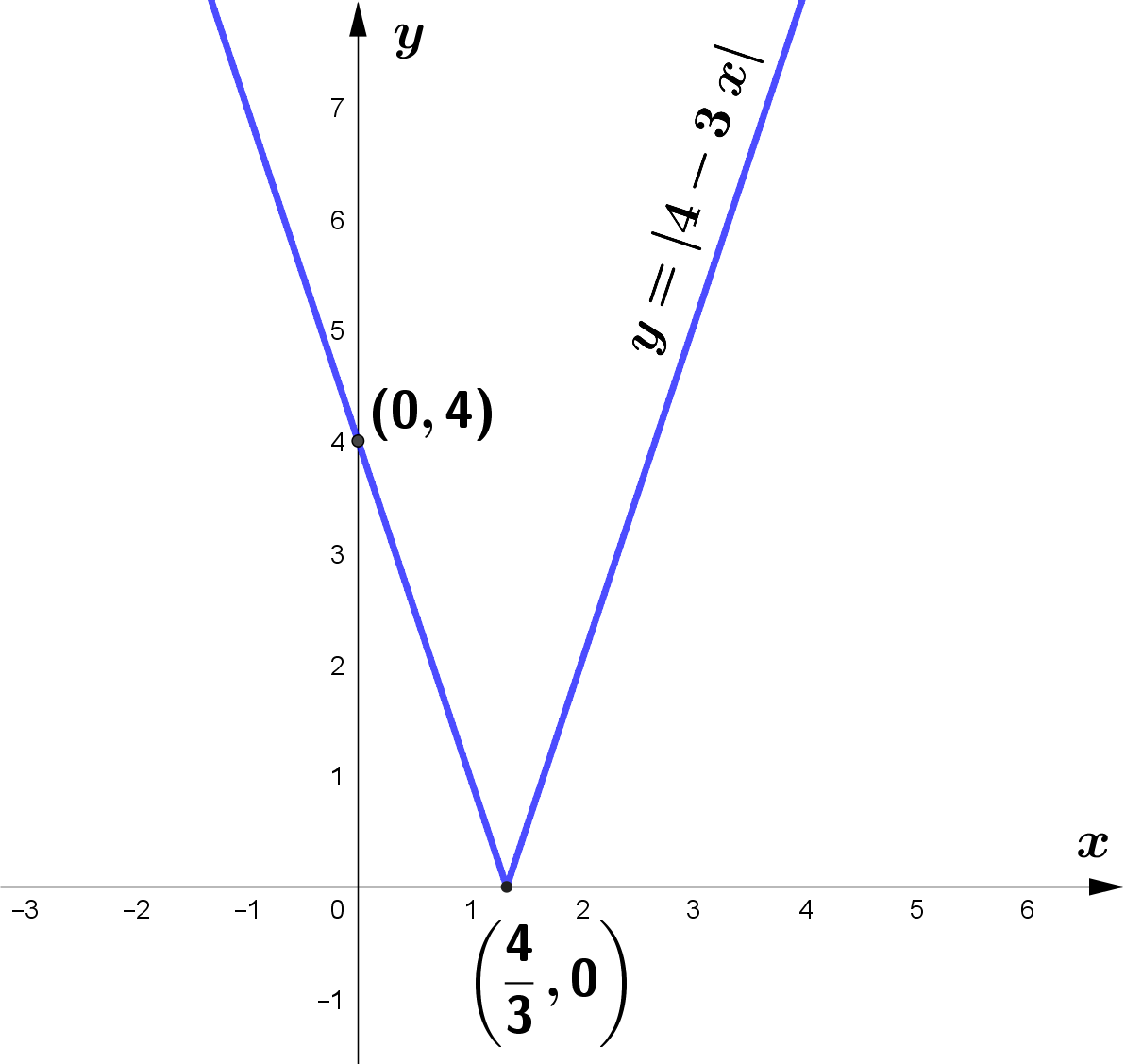
2. (a) On the axes, sketch the graph of $y=|4-3 x|$, stating the intercepts with the coordinate axes. [2]
   (b) Solve the inequality $|4-3 x|\ge 7$. [3]
   






$\begin{aligned} y&=|4-3 x|\\\\ &=\left|-3\left(x-\frac{4}{3}\right)\right| \\\\ &=|-3|\left|\left(x-\frac{4}{3}\right)\right| \\\\ &=3\left|x-\frac{4}{3}\right|\\\\ \end{aligned}$ $\therefore$ The vertex point is $\left(\dfrac{4}{3}, 0\right)\\\\\\\\ $ When $x=0, y=3\left|0-\dfrac{4}{3}\right|=4\\\\\\\\ $. $\therefore$ The $y$-intercept is $(0,4).$ $\begin{aligned} |4-3 x| & \geq 7 \\\\ 3\left|x-\frac{4}{3}\right| & \geq 7 \\\\ \left|x-\frac{4}{3}\right| & \geq \frac{7}{3} \\\\ x-\frac{4}{3} & \leq-\frac{7}{3} \text { or } x-\frac{4}{3} \geq \frac{7}{3} \\\\ x & \leq-1 \text { or } x \geq \frac{11}{3} \end{aligned}$




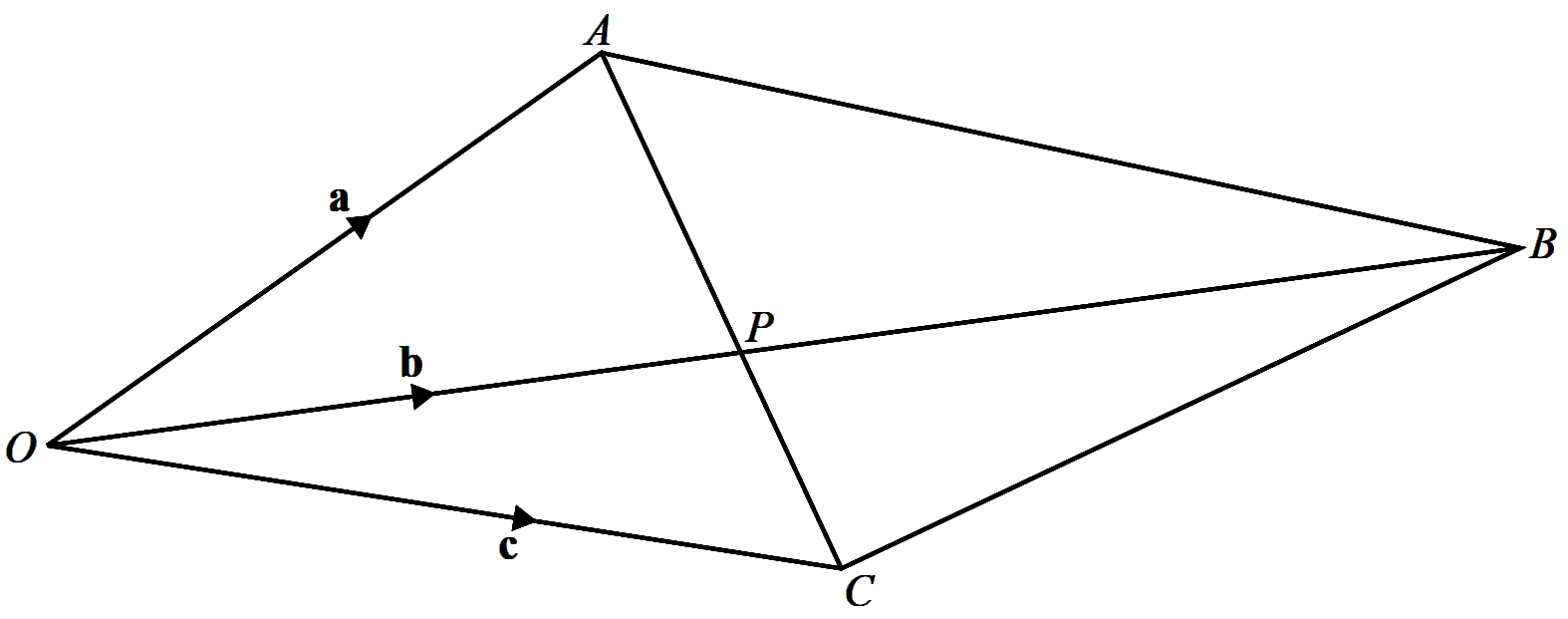
3. The diagram shows the quadrilateral $O A B C$ such that $\overrightarrow{O A}=\mathbf{a}, \overrightarrow{O B}=\mathbf{b}$ and $\overrightarrow{O C}=\mathbf{c}$. The lines $O B$ and $A C$ intersect at the point $P$, such that $A P: P C=3: 2$.
   (a) Find $\overrightarrow{O P}$ in terms of $\mathbf{a}$ and $\mathbf{c}$. [3]
   (b) Given also that $O P: P B=2: 3$, show that $2 \mathbf{b}=3 \mathbf{c}+2 \mathbf{a}$. [2]






$\begin{aligned} A P: P C &=3: 2 \\\\ \overrightarrow{O P} &=\frac{1}{5}(2 \overrightarrow{O A}+3 \overrightarrow{O C}) \\\\ &=\frac{1}{5}(2 \vec{a}+3 \vec{c})\\\\ \end{aligned}$ $O P: P B=2: 3$ and $O, P, B$ are collinear. $\begin{aligned} &\\ \therefore 3 \overrightarrow{O P} &=2 \overrightarrow{P B} \\\\ \therefore \overrightarrow{P B} &=\frac{3}{2} \overrightarrow{O P} \\\\ &=\frac{3}{10}(2 \vec{a}+3 \vec{c}) \\\\ \overrightarrow{O B} &=\overrightarrow{O P}+\overrightarrow{P B} \\\\ \vec{b} &=\frac{1}{5}(2 \vec{a}+3 \vec{c})+\frac{3}{10}(2 \vec{a}+3 \vec{c}) \\\\ &=\frac{1}{2}(2 \vec{a}+3 \vec{c}) \\\\ \therefore 2\vec{b} &=2 \vec{a}+3 \vec{c} \end{aligned}$




4. A curve is such that $\dfrac{d^{2} y}{d x^{2}}=(3 x+2)^{-\frac{1}{3}}$. The curve has gradient $4$ at the point $(2,6.2)$. Find the equation of the curve. [6]






$\begin{aligned} \frac{d^{2} y}{d x^{2}} &=(3 x+2)^{-\frac{1}{3}} \\\\ \therefore\ \frac{d y}{d x} &=\displaystyle\int(3 x+2)^{-\frac{1}{3}} d x \\\\ \text { Let } u &=3 x+2 \\\\ d u &=3 d x \\\\ d x &=\frac{1}{3} d u\\\\ \therefore\ & \quad \displaystyle\int(3 x+2)^{-\frac{1}{3}} d x \\\\ &=\frac{1}{3} \displaystyle\int u^{-\frac{1}{3}} d u \\\\ &=\frac{1 / 3}{2 / 3} u^{2 / 3}+9 \\\\ &=\frac{1}{2} u^{2 / 3}+c_{1} \\\\ \therefore\ \frac{d y}{d x} &=\frac{1}{2}(3 x+2)^{\frac{2}{3}}+c_{1}\\\\ \left.\frac{d y}{d x}\right|_{(2,6.2)} &=4 \\\\ \frac{1}{2}(6+2)^{\frac{2}{3}}+c_{1} &=4 \\\\ 2+c_{1} &=4 \\\\ \therefore\ c_{1} &=2 \\\\ \therefore\ \frac{d y}{d x} &=\frac{1}{2}(3 x+2)^{\frac{2}{3}}+2\\\\ y &=\displaystyle\int\left[\frac{1}{2}(3 x+2)^{\frac{2}{3}}+2\right] d x \\\\ &=\frac{1}{2} \displaystyle\int(3 x+2)^{\frac{2}{3}} d x+2 \int d x \\\\ &=\frac{1}{2} \times \frac{1}{3} \displaystyle\int(3 x+2)^{\frac{2}{3}} d(3 x+2)+2 \int d x \\\\ &=\frac{1}{10}(3 x+2)^{\frac{5}{3}}+2 x+c_{2}\\\\ \text{ When } x&=2, y=6.2\\\\ &6 \cdot 2=\frac{1}{10}(6+2)^{\frac{5}{3}}+4+c_{2} \\\\ &6 \cdot 2=3 \cdot 2+4+c_{2}\\\\ &\therefore\ c_{2}=-1 \\\\ &\therefore\ y=\frac{1}{10}(3 x+2)^{\frac{5}{3}}+2 x-1 \end{aligned}$




5. (a) Given that $\log _{a} p+\log _{a} 5-\log _{a} 4=\log _{a} 20$, find the value of $p$. [2]
   (b) Solve the equation $3^{2 x+1}+8\left(3^{x}\right)-3=0$. [3]
   (c) Solve the equation $4 \log _{y} 2+\log _{2} y=4$. [3]






$\begin{aligned} \text { (a) }\quad \log _{a} p+\log _{a} 5-\log _{a} 4 &=\log _{a} 20 \\\\ \log _{a}\left(\frac{5 p}{4}\right) &=\log _{a} 20 \\\\ \therefore \quad \frac{5 p}{4} &=20 \\\\ 5 p &=80 \\\\ p &=16\\\\ \text { (b) }\quad \qquad 3^{2 x+1}+8\left(3^{x}\right)-3&=0\\\\ 3^{2 x} \cdot 3+8\left(3^{x}\right)-3&=0 \\\\ 3\left(3^{x}\right)^{2}+8\left(3^{x}\right)-3&=0 \\\\ \left(3 \cdot 3^{x}-1\right)\left(3^{x}+3\right)&=0 \\\\ 3^{x}=\frac{1}{3} \text { or } 3^{x}&=-3\\\\ \end{aligned}$ $\qquad$ Since $3^{x}>0$ for all $x \in \mathbb{R}$, $3^{x}=-3$ has no solution. $\begin{aligned} &\\ \qquad 3^{x}&=\frac{1}{3} \\\\ 3^{x}&=3^{-1} \\\\ x&=-1\\\\ \end{aligned}$ $\begin{aligned} \text { (c) } \qquad 4 \log _{y} 2+\log _{2} y &=4 \\\\ \frac{4}{\log _{2} y}+\log _{2} y &=4 \\\\ 4+\left(\log _{2} y\right)^{2} &=4 \cdot \log _{2} y \\\\ \left(\log _{2} y\right)^{2}-4 \log y+4 &=0 \\\\ \left(\log _{2} y-2\right)^{2} &=0 \\\\ \log _{2} y &=2 \\\\ y &=4 \end{aligned}$




6. DO NOT USE A CALCULATOR IN THIS QUESTION.
   A curve has equation $y=(3+\sqrt{5}) x^{2}-8 \sqrt{5} x+60$.
   (a) Find the $x$-coordinate of the stationary point on the curve, giving your answer in the form $a+b \sqrt{5}$, where $a$ and $b$ are integers. [4]
   (b) Hence find the $y$-coordinate of this stationary point, giving your answer in the form $c \sqrt{5}$, where $c$ is an integer. [3]
   






$\begin{aligned} &y =(3+\sqrt{5}) x^{2}-8 \sqrt{5} x+60 . \\\\ &\frac{d y}{d x} =2(3+\sqrt{5}) x-8 \sqrt{5}\\\\ \end{aligned}$ At stationary point, $\begin{aligned} &\\ \frac{d y}{d x} &=0 \\\\ 2(3+\sqrt{5}) x-8 \sqrt{5} &=0 \\\\ x &=\frac{8 \sqrt{5}}{2(3+\sqrt{5})}\\\\ &=\frac{4 \sqrt{5}}{3+\sqrt{5}} \\\\ &=\frac{4 \sqrt{5}}{3+\sqrt{5}} \times \frac{3-\sqrt{5}}{3-\sqrt{5}} \\\\ &=\frac{12 \sqrt{5}=20}{9-5} \\\\ &=\frac{12 \sqrt{5}-20}{4} \\\\ &=-5+3 \sqrt{5}\\\\ \end{aligned}$ When $x=-5+3 \sqrt{5}$, $\begin{aligned} &\\ y &=(3+\sqrt{5})(-5+3 \sqrt{5})^{2}-8 \sqrt{5}(-5+3 \sqrt{5})+60 \\\\ &=(3+\sqrt{5})(25-30 \sqrt{5}+45)+40 \sqrt{5}-120+60 \\\\ &=(3+\sqrt{5})(70-30 \sqrt{5})+40 \sqrt{5}-60 \\\\ &=210-90 \sqrt{5}+70 \sqrt{5}-150+40 \sqrt{5}-60 \\\\ &=20 \sqrt{5}\\\\ \end{aligned}$




7. (a) A six-character password is to be made from the following eight characters.
   
   $\begin{array}{llllll}\text { Digits } & \quad 1\quad & \quad 3\quad & \quad 5\quad & \quad 8\quad & \quad 9\quad \\\\ \text { Symbols } & \quad * \quad & \quad \$ \quad & \quad \# \quad & & \end{array}$
   
   No character may be used more than once in a password. Find the number of different passwords that can be chosen if
   (i) there are no restrictions, [1]
   (ii) the password starts with a digit and finishes with a digit, [2]
   (iii) the password starts with three symbols. [2]
   (b) The number of combinations of 5 objects selected from $n$ objects is six times the number of combinations of 4 objects selected from $n-1$ objects. Find the value of $n$. [3]






$\text{ (a) }$ (i) number of ways to form different passwords $={}^8P_{6}=20160$ ways. $\quad\ $ (ii) number of ways to form different passwords starting with a digit and ending with a digit. $={}^5P_{2} \times{ }^{6}P_{4}=7200$ ways. $\quad\ $ (iii) number of ways to form different passwords starting with three symbols $=3 ! \times {}^5P_{3}=360 $ ways. $\begin{aligned} &\\ \text{ (b) } \hspace{2cm} { }^{n} C_{5} &=6 \times{ }^{n-1} C_{4} \\\\ \frac{n !}{5 !(n-5) !} &=6 \times \frac{(n-1) !}{4 !(n-1-4) !} \\\\ \frac{n(n-1) !}{5 \times 4 !(n-5) !} &=\frac{6 \times(n-1) !}{4 !(n-5) !} \\\\ \frac{n}{5} &=6 \\\\ n &=30 \end{aligned}$




8. Variables $x$ and $y$ are such that $y=A x^{b}$, where $A$ and $b$ are constants. When $\lg y$ is plotted against $\lg x$, a straight line graph passing through the points $(0.61,0.57)$ and $(5.36,4.37)$ is obtained.
   (a) Find the value of $A$ and of $b$. [5]
   Using your values of $A$ and $b$, find
   (b) the value of $y$ when $x=3$, [2]
   (c) the value of $x$ when $y=3$. [2]






$\begin{aligned} \text{ (a) }\quad y &=A x^{b} \\\\ \lg y &=\lg \left(A x^{b}\right) \\\\ \lg y &=\lg A+b \lg x \\\\ 0.57 &=\lg A+0.616 \ldots(1) \\\\ 5.36 &=\lg A+4.37 b \ldots(2)\\\\ \end{aligned}$ $\quad$ Solving equations $(1)$ and $(2)$ $\begin{aligned} &\\ b &=0.8 \\\\ \lg A &=0.082 \\\\ A &=10^{0.082} \\\\ &=1.21\\\\ \therefore\ y&=1.21\left(x^{0.8}\right)\\\\ \text{ (b) }\quad \text{ When } x&=3\\\\ y &=1.21(3)^{0.8} \\\\ &=2.91 \\\\ \text{ (c) }\quad \text { When } y &=3, \\\\ 3 &=1.21\left(x^{0.8}\right) \\\\ x^{0.8} &=\frac{3}{1.21} \\\\ x &=\left(\frac{3}{1.21}\right)^{1.25} \\\\ &=3.11 \end{aligned}$




9. (a) The first three terms of an arithmetic progression are $-4,8,20$. Find the smallest number of terms for which the sum of this arithmetic progression is greater than 2000. [4]
   (b) The $7^{\text{ th}}$ and $9^{\text{ th}}$ terms of a geometric progression are $27$ and $243$ respectively. Given that the geometric progression has a positive common ratio, find
   (i) this common ratio, [2]
   (ii) the $30^{\text{ th}}$ term, giving your answer as a power of $3 .$ [2]
   (c) Explain why the geometric progression $1, \sin \theta, \sin ^{2} \theta, \ldots$ for $-\dfrac{\pi}{2}<\theta<\dfrac{\pi}{2}$, where $\theta$ is in radians, has a sum to infinity. [2]
   






$\text{ (a) } \quad -4,8,20, \ldots$ is an A.P. $\begin{aligned} &\\ \therefore\ a &=-4 \\\\ d &=8-(-4) \\\\ &=12 \\\\ S_{n} &>2000 \\\\ \frac{n}{2}\{2 a+(n-1) d\} &>2000 \\\\ \frac{n}{2}\{-8+(n-1) 12\} &>2000 \\\\ n\{-2+3 n-3\} &>1000\\\\ 3 n^{2}-5 n &>1000 \\\\ n^{2}-\frac{5}{3} n &>\frac{1000}{3} \\\\ n-\frac{5}{3} n+\left(\frac{5}{6}\right)^{2} &>\frac{1000}{3}+\left(\frac{5}{6}\right)^{2} \\\\ \left(n-\frac{5}{6}\right)^{2} &>334.03 \\\\ n-\frac{5}{6} &>18.28 \\\\ n &>19.1 \\\\ \therefore n &=20\\\\ \end{aligned}$ $\therefore$ The smalles number of terms $=20\\\\ $ $\text{ (b) }$ In a G.P, $\begin{aligned} &\\ \text{ (i) } \quad u_{7} &=27 \\\\ a r^{6} &=27 \cdots(1) \\\\ u_{9} &=243 \\\\ a r^{8} &=243 \cdots(2) \\\\ \frac{a r^{8}}{a r^{6}}&= \frac{243}{27} \\\\ r^{2} &=9 \\\\ \therefore\ r &=3\\\\ \therefore\ a\left(3^{6}\right) &=27 \\\\ a &=\frac{3^{3}}{3^{6}} \\\\ &=\frac{1}{3^{3}} \\\\ u_{30} &=a r^{29} \\\\ &=\frac{1}{3^{3}} \times 3^{29} \\\\ &=3^{26}\\\\ \end{aligned}$ $\text{ (c) } \quad 1, \sin \theta, \sin ^{2} \theta, \ldots$ is a GP, where $\begin{aligned} &\\ &r =\frac{\sin \theta}{1} \\\\ &\ \ =\sin \theta \\\\ &\text { Since }-\frac{\pi}{2}<\theta <\frac{\pi}{2}\\\\ &\sin \left(-\frac{\pi}{2}\right)<\sin \theta <\sin \frac{\pi}{2} \\\\ &-1< r <1 \\\\ &\therefore\ |r| <1\\\\ \end{aligned}$ Hence, the series is convergent and sum to infinity exists.




10. (a) Solve the equation $\sin \alpha \operatorname{cosec}^{2} \alpha+\cos \alpha \sec ^{2} \alpha=0$ for $-\pi<\alpha<\pi$, where $\alpha$ is in radians. [4]
    (b) (i) Show that $\dfrac{\cos \theta}{1-\sin \theta}+\dfrac{1-\sin \theta}{\cos \theta}=2 \sec \theta$. [4]
    (ii) Hence solve the equation $\dfrac{\cos 3 \phi}{1-\sin 3 \phi}+\dfrac{1-\sin 3 \phi}{\cos 3 \phi}=4$ for $0^{\circ} \leq \phi \leq 180^{\circ}$. [4]






$\begin{aligned} \text{ (a) }\quad\sin \alpha \operatorname{cosec}^{2} \alpha+\cos \alpha \sec ^{2} \alpha & =0,-\pi<\alpha<\pi\\\\ \frac{1}{\sin \alpha}+\frac{1}{\cos \alpha} &=0 \\\\ \frac{1}{\cos \alpha} &=-\frac{1}{\sin \alpha} \\\\ \therefore \frac{\sin \alpha}{\cos \alpha} &=-1 \\\\ \tan \alpha &=-1 \\\\ \alpha=-\frac{\pi}{4} \quad \text { or } \alpha &=\frac{3 \pi}{4}\\\\ \end{aligned}$ $\begin{aligned} \text{ (b) (i) }\quad & \frac{\cos \theta}{1-\sin \theta}+\frac{1-\sin \theta}{\cos \theta} \\\\ =&\ \frac{\cos ^{2} \theta+1-2 \sin \theta+\sin ^{2} \theta}{(1-\sin \theta) \cos \theta} \\\\ =&\ \frac{2-2 \sin \theta}{(1-\sin \theta) \cos \theta} \\\\ =&\ \frac{2(1-\sin \theta)}{(1-\sin \theta) \cos \theta} \\\\ =&\ \frac{2}{\cos \theta}=2 \sec \theta\\\\ \end{aligned}$ $\text{ (ii) }\quad\dfrac{\cos 3 \phi}{1-\sin 3 \phi}+\dfrac{1-\sin 3 \phi}{\cos 3 \phi}=4\\\\ $ $\qquad$ By part (i), $\begin{aligned} &\\ \frac{2}{\cos 3 \phi} &=4 \\\\ \cos 3 \phi &=\frac{1}{2} \\\\ 3 \phi=60^{\circ} \text { or } 3 \phi &=300^{\circ} \text { or } 3 \phi=420^{\circ} \\\\ \phi=20^{\circ} \text { or } \phi &=100^{\circ} \text { or } \phi=140^{\circ} \end{aligned}$




11. The normal to the curve $y=\dfrac{\ln \left(x^{2}+2\right)}{2 x-3}$ at the point where $x=2$ meets the $y$-axis at the point $P$. Find the coordinates of $P$. [7]






$\begin{aligned} \text{Curve }: y&=\dfrac{\ln \left(x^{2}+2\right)}{2 x-3}\\\\ \dfrac{d y}{d x} &=\dfrac{(2 x-3) \dfrac{d}{d x} \ln \left(x^{2}+2\right)-\ln \left(x^{2}+2\right) \dfrac{d}{d x}(2 x-3)}{(2 x-3)^{2}} \\\\ &=\dfrac{(2 x-3) \dfrac{2 x}{x^{2}+2}-2 \ln \left(x^{2}+2\right)}{(2 x-3)^{2}} \\\\ &=\dfrac{2}{(2 x-3)^{2}}\left[\dfrac{x(2 x-3)}{x^{2}+2}-\ln \left(x^{2}+2\right)\right]\\\\ \end{aligned}$ $\begin{aligned} \left.\dfrac{d y}{d x}\right|_{x=2} &=\dfrac{2}{(4-3)^{2}}\left[\dfrac{2(4-3)}{4+2}-\ln (4+2)\right] \\\\ &=2\left[\dfrac{1}{3}-\ln 6\right] \\\\ &=\dfrac{2(1-3 \ln 6)}{3} \\\\ \therefore \text { Gradient of normal } &=-\dfrac{3}{2(1-3 \ln 6)} \\\\ &=\dfrac{3}{2(3 \ln 6-1)}\\\\ \text{ When } x&=2,\\\\ y&=\ln 6\\\\ \end{aligned}$ $\therefore$ The equation of normal at $(2, \ln 6)$ is $\begin{aligned} &\\ y-\ln 6 &=\dfrac{3}{2(3 \ln 6-1)}(x-2) \\\\ y &=\dfrac{3}{2(3 \ln 6-1)}(x-2)+\ln 6\\\\ \text{ When } x&=0,\\\\ y &=\dfrac{3}{1-3 \ln 6}+\ln 6 \\\\ &=1.11\\\\ \end{aligned}$ $\therefore$ The coordinates of the point $P$ is $(0,1.11).$

စာဖတ်သူ၏ အမြင်ကို လေးစားစွာစောင့်မျှော်လျက်!