-
The equation of a curve is such that dydx=3x4+32x3. It is given that the curve passes through the point (12,4). Find the equation of the curve. [4]
-
The sum of the first 20 terms of an arithmetic progression is 405 and the sum of the first 40 terms is 1410 .Find the 60^{\text{th}} term of the progression. [5]
-
(a) Find the first three terms in the expansion of (3 - 2x)^5 in ascending powers of x. [3]
(b) Hence find the coefficient of x^2 in the expansion of (4 + x)^2(3-2x)^5.[3] [4] -
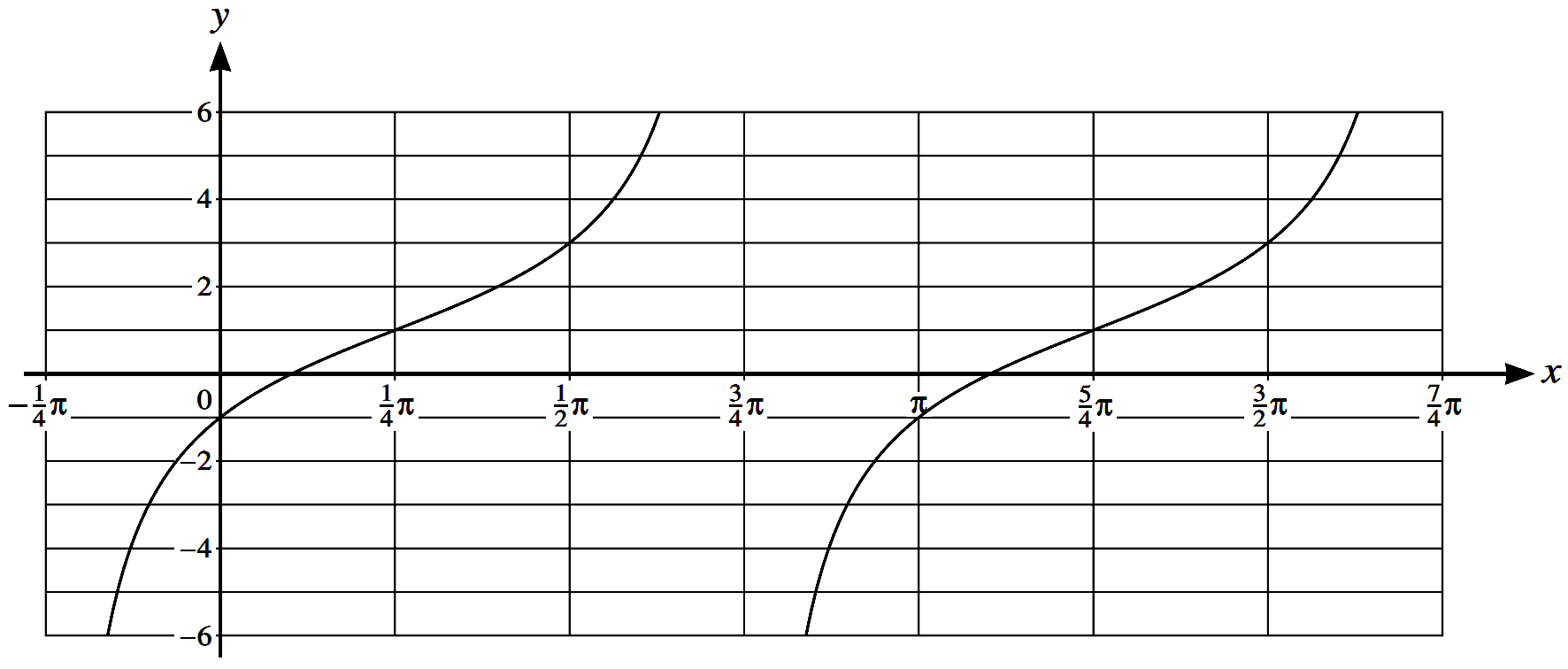
The diagram shows part of the graph of y = a \tan (x - b) + c. Given that 0 < b < \pi, state the values of the constants a, b and c. [4]
-
The fifth, sixth and seventh terms of a geometric progression are 8k, -12 and 2k respectively.Given that k is negative, find the sum to infinity of the progression. [4]
-
The equation of a curve is y = (2k - 3)x^2 - kx - (k - 2), where k is a constant. The line y = 3x - 4 is a tangent to the curve. Find the value of k. [5]
-
(a) Prove the identity \dfrac{1-2 \sin ^{2} \theta}{1-\sin ^{2} \theta} \equiv 1-\tan ^{2} \theta. [2]
(b) Hence solve the equation \dfrac{1-2 \sin ^{2} \theta}{1-\sin ^{2} \theta}=2 \tan ^{4} \theta for 0^{\circ} \leq \theta \leq 180^{\circ}. [3]
-
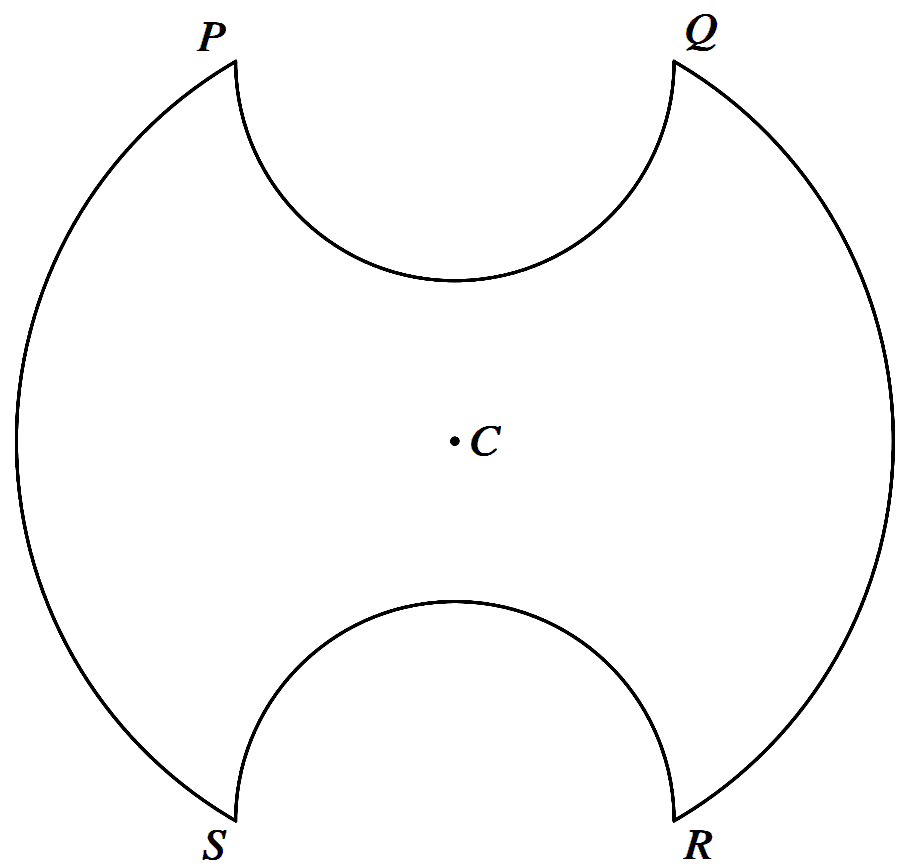
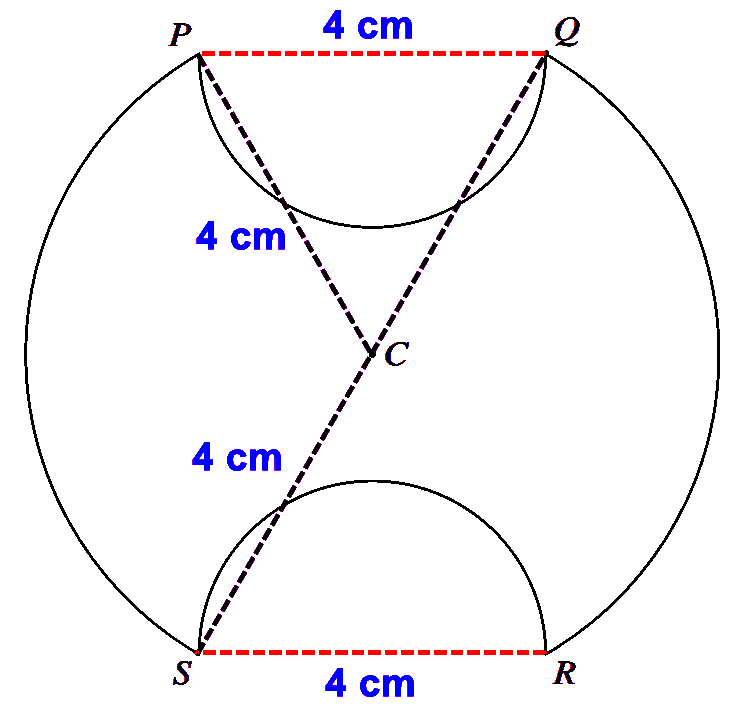
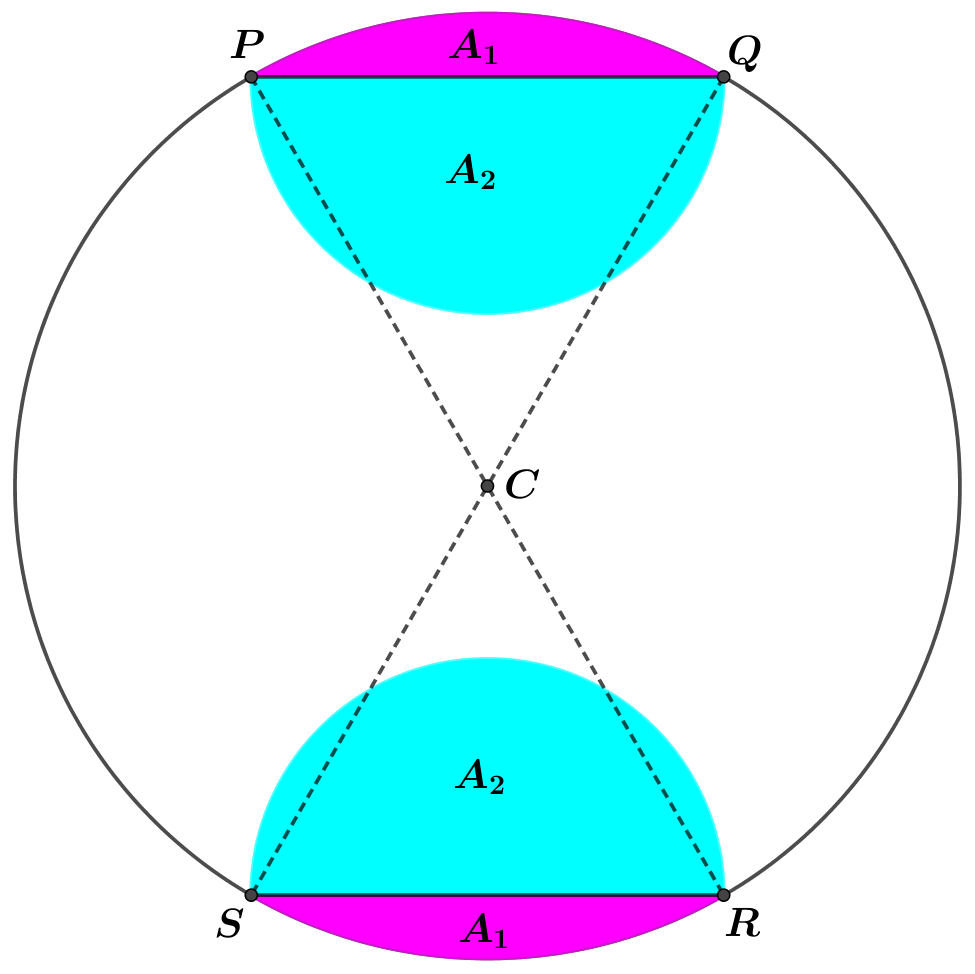
The diagram shows a symmetrical metal plate. The plate is made by removing two identical piecesfrom a circular disc with centre C. The boundary of the plate consists of two arcs PS and QR of the original circle and two semicircles with PQ and RS as diameters. The radius of the circle with centre C is 4 cm, and PQ = RS = 4 cm also.
(a) Show that angle PCS = \dfrac{2}{3}\pi radians. [2]
(b) Find the exact perimeter of the plate. [3]
(c) Show that the area of the plate is \left(\dfrac{20}{3} \pi+8 \sqrt{3}\right) \mathrm{cm}^{2}. [5] -
Functions f and g are defined as follows:
\begin{aligned} &\\ &f(x)=(x-2)^{2}-4 \text { for } x \geq 2 \\\\ &g(x)=a x+2 \text { for } x \in \mathbb{R}\\\\ \end{aligned}
where a is a constant.
(a) State the range of f. [1]
(b) Find f^{-1}(x). [2]
(c) Given that a = -\dfrac{5}{3}, solve the equation f(x) = g(x). [3]
(d) Given instead that ggf^{-1}(12) = 62, find the possible values of a. [5] -
The equation of a circle is x^2 + y^2 - 4x + 6y - 77 = 0.
(a) Find the x-coordinates of the points A and B where the circle intersects the x-axis. [2]
(b) Find the point of intersection of the tangents to the circle at A and B.
[6] -
The equation of a curve is y=2 \sqrt{3 x+4}-x.
(a) Find the equation of the normal to the curve at the point (4,4), giving your answer in the form y=m x+c. [5]
(b) Find the coordinates of the stationary point. [3]
(c) Determine the nature of the stationary point. [2]
(d) Find the exact area of the region bounded by the curve, the x-axis and the lines x = 0 and x = 4. [4]